¶ 1994 AMC8 Problem 19
Problem:
Around the outside of a by square, construct four semicircles (as shown in the figure) with the four sides of the square as their diameters. Another square, , has its sides parallel to the corresponding sides of the original square, and each side of is tangent to one of the semicircles. The area of the square is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The radius of each semicircle is , since it is the length of a side of the by square. Since the length of a side of is the length of a side of the by square plus two radii of semicircles [see figure], each side of measures , so the area of is .
.jpg)
Complete each semicircle to a circle, and note that since the radius of each circle is half the side-length of the smaller square, the four circles must intersect at the center of both squares. Thus, since the length of is the length of two diameters. Hence, the area of is .
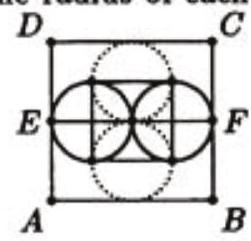
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions