Problem:
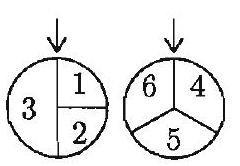
The two wheels shown at the right are spun and the two resulting numbers are added. The probability that the sum of the two numbers is even is
Answer Choices:
A. 61
B. 41
C. 31
D. 125
E. 94
Solution:
Subdivide the 3-space on the first wheel so that wheel is divided into four equal regions. Each of the four regions has the same probability of occurring when the first wheel is spun. Hence, the sample space is
(1,4)(2,4)(3,4)(3,4)(1,5)(2,5)(3,5)(3,5)(1,6)(2,6)(3,6)(3,6)
The final three entries were repeated to show the double space for 3 on the first wheel. The sums for these entries are 5,6,7,6,7,8,7,8,9,7,8,9. Five of these twelve are even.
OR
There are two ways to get an even sum, (odd + odd) or (even + even). The first outcome happens if one spins 1 or 3 on the first wheel (3 chances out of 4) and 5 on the second wheel (1 chance out of 3) for a probability of 43×31=41. The second outcome happens if one spins a 2 on the first wheel (1 chance out of 4) and 4 or 6 on the second wheel (2 chances out of 3) for a probability of 41×32=61. Thus the total probability of an even sum is 41+61=125.
OR
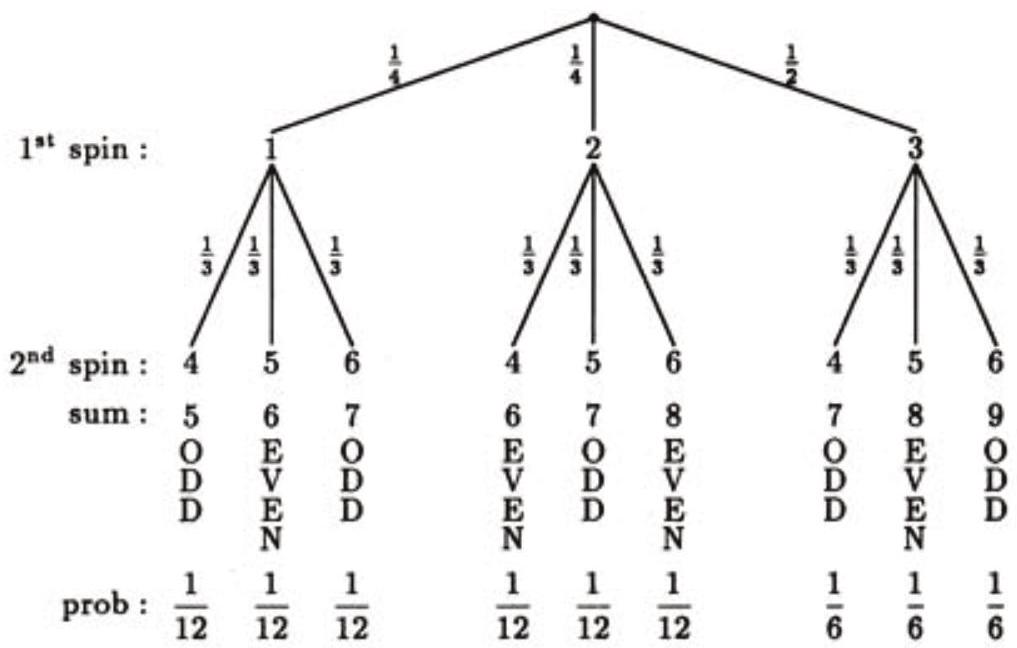
Use a probability tree diagram:
Thus, the probability that the sum is even is 121+121+121+61=125.
OR
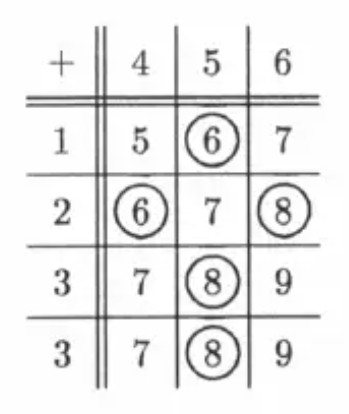
List equally likely outcomes in a table. Even sums are marked. The probability is 5/12.
OR
P(even)=P(3+5)+P(1+5)+P(2+4)+P(2+6)=(21)(31)+(41)(31)+(41)(31)+(41)(31)=125.
Answer: D.
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)