¶ 1996 AMC8 Problem 16
Problem:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Combining in groups of four yields
and so on. Since there are groups of four in , it follows that the sum is zero.
Combining in pairs yields
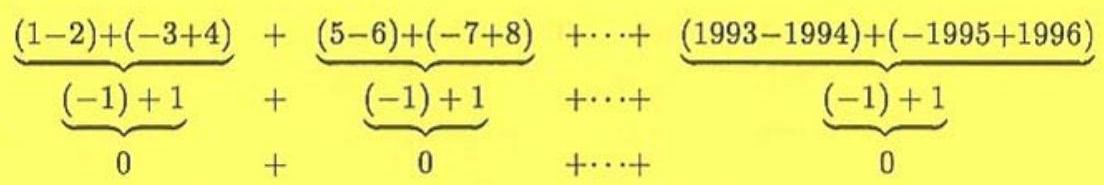
so the sum is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions