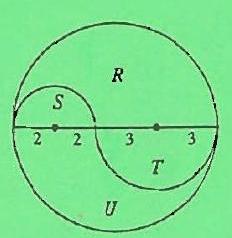
Problem:
ACE is divided at C in the ratio 2:3. The two semicircles, ABC and CDE, divide the circular region into an upper (shaded) region and a lower region. The ratio of the area of the upper region to that of the lower region is
Answer Choices:
A. 2:3
B. 1:1
C. 3:2
D. 9:4
E. 5:2
Solution:
Let the diameter of the large circle equal 10. Then the ratio is:
(Area of semicircle T+U)β(Area of semicircle T)+(Area of semicircle S)(Area of semicircle R+S)β(Area of semicircle S)+(Area of semicircle T)β=21βΟ52β21βΟ32+2221βΟ52β21βΟ22+21βΟ32β=10Ο15Οβ=23β or 3:2.
Answer: Cβ.
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)
