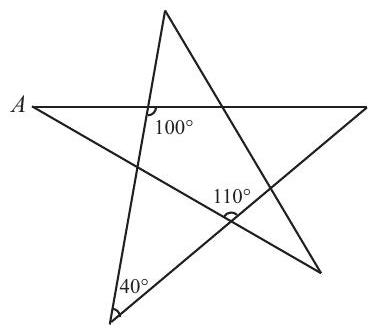
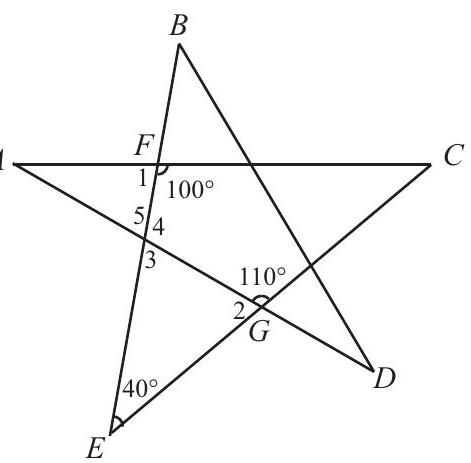
Problem:
The degree measure of angle A is
Answer Choices:
A. 20
B. 30
C. 35
D. 40
E. 45
Solution:
Since ∠1 forms a straight line with angle 100∘,∠1=80∘. Since ∠2 forms a straight line with angle 110∘,∠2=70∘. Angle 3 is the third angle in a triangle with ∠E=40∘ and ∠2=A 70∘, so ∠3=180∘−40∘−70∘=70∘.Angle 4= 110∘ since it forms a straight angle with ∠3. Then ∠5 forms a straight angle with ∠4, so ∠5=70∘. (Or ∠3=∠5 because they are vertical angles.) Therefore, ∠A=180∘−∠1−∠5=180∘−80∘− 70∘=30∘.
OR
The angle sum in △CEF is 180∘, so ∠C=180∘− 40∘−100∘=40∘. In △ACG,∠G=110∘ and ∠C=40∘, so ∠A=180∘−110∘−40∘=30∘.
Answer: B.
The problems on this page are the property of the MAA's American Mathematics Competitions