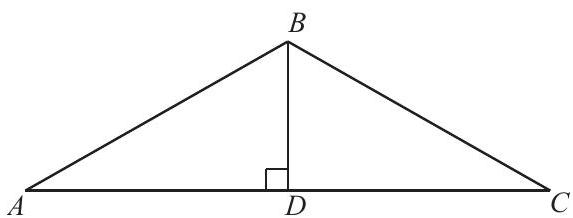
Problem:
The base of isosceles △ABC is 24 and its area is 60. What is the length of one of the congruent sides?
Answer Choices:
A. 5
B. 8
C. 13
D. 14
E. 18
Solution:
Let BD be the altitude from B to AC in △ABC.
Then 60= the area of △ABC=21⋅24⋅BD, so BD=5. Because △ABC is isosceles, △ABD and △CBD are congruent right triangles. This means that AD=DC=224=12. Applying the Pythagorean Theorem to △ABD gives
AB2=52+122=169=132, so AB=13.
Answer: C.
The problems on this page are the property of the MAA's American Mathematics Competitions