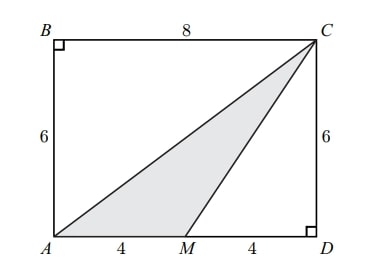
Problem:
In rectangle ABCD,AB=6 and AD=8. Point M is the midpoint of AD. What is the area of △AMC?
Answer Choices:
A. 12
B. 15
C. 18
D. 20
E. 24
Solution:
The area of △ACD is 21⋅8⋅6=24. The area of △MCD is 21⋅4⋅6=12. So the area of △AMC is 24−12=12.
OR
As seen in the diagram above, the altitude from C to the line of the base AM is CD. Thus the area of the shaded △AMC is
21⋅AM⋅CD=21⋅4⋅6=12.
Answer: A.
The problems on this page are the property of the MAA's American Mathematics Competitions