¶ 2016 AMC8 Problem 23
Problem:
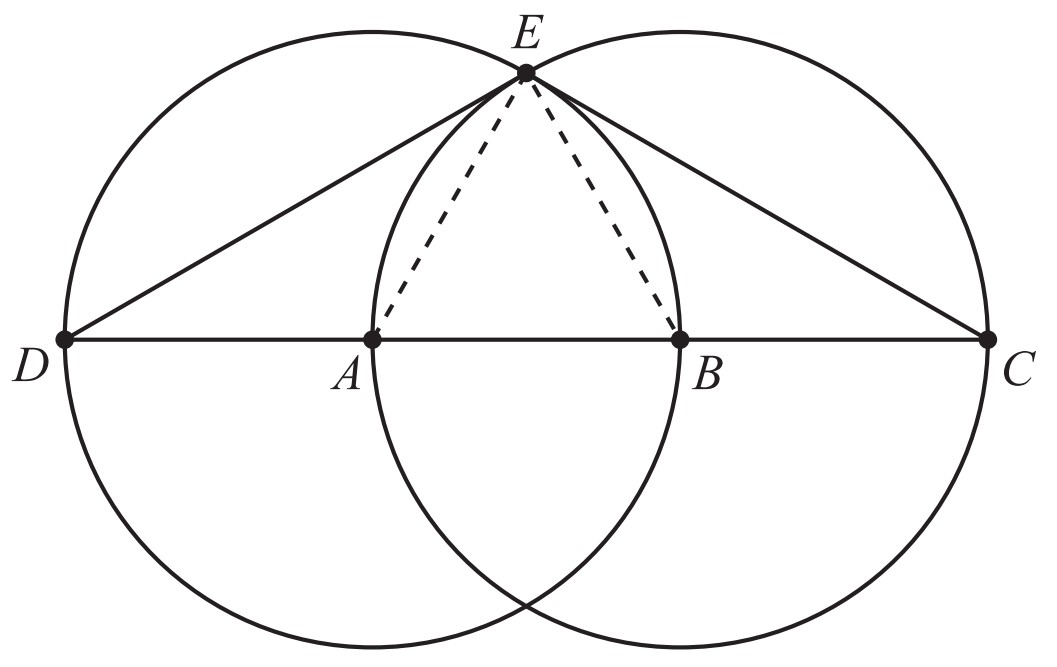
Two congruent circles centered at points and each pass through the other's center. The line containing both and is extended to intersect the circles at points and . The two circles intersect at two points, one of which is . What is the degree measure of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
We know is equilateral since each of its sides is a radius of one of the congruent circles. Thus the measure of is . Since is a diameter of circle and is a diameter of circle , it follows that and are both right angles. Therefore the degree measure of is .
We know is equilateral since each of its sides is a radius of one of the congruent circles. Thus the measures of and are both . Then the measure of is , and since is isosceles, the measure of is . Similarly, the measure of is also . Therefore the degree measure of is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions