Problem:
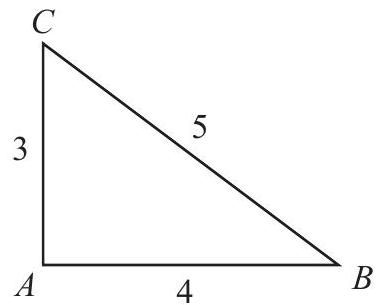
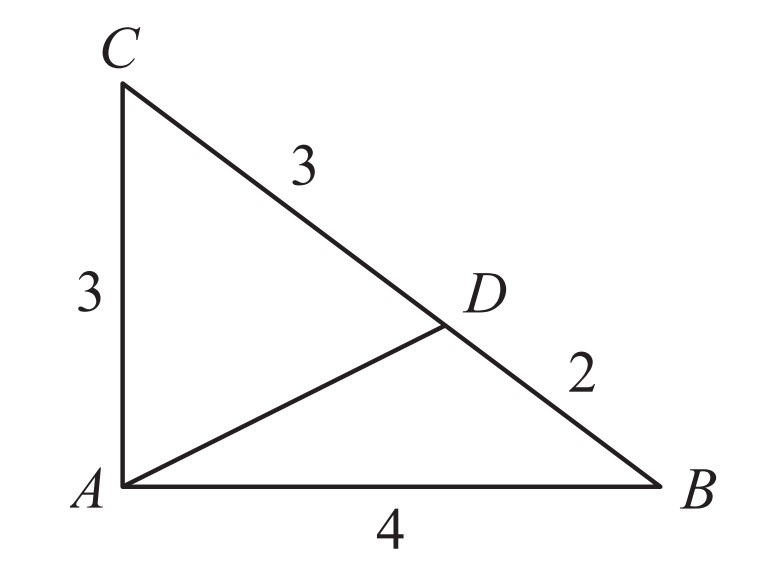
In the figure shown below, choose point D on side BC so that △ACD and △ABD have equal perimeters. What is the area of △ABD?
Answer Choices:
A. 43
B. 23
C. 2
D. 512
E. 25
Solution:
Because the perimeters of △ADC and △ADB are equal, CD=3 and BD=2.
△ADC and △ADB have the same altitude from A, so the area of △ADC will be 3/5 of the area of △ABC, and △ADB will be 52 of the area of △ABC. The area of △ABC is 21⋅3⋅4=6, so the area of △ADB is 52⋅6=12/5.
Answer: D.
The problems on this page are the property of the MAA's American Mathematics Competitions