¶ 2018 AMC8 Problem 15
Problem:
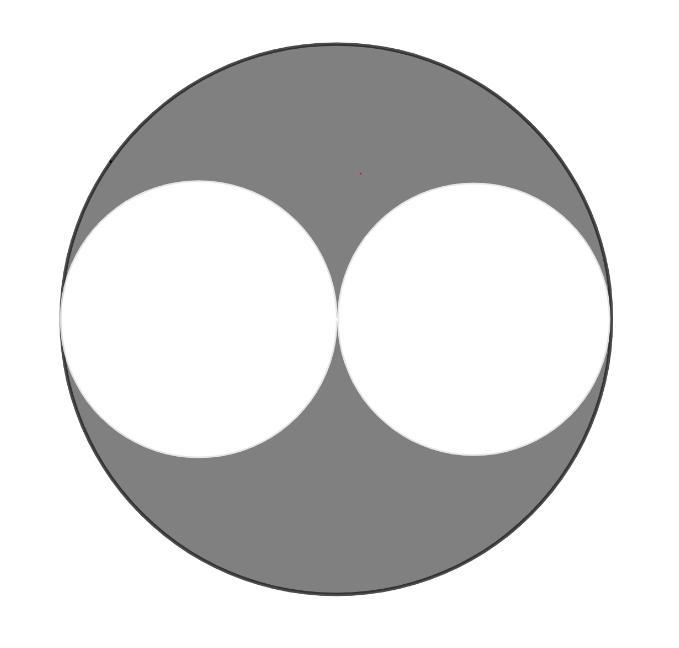
In the diagram below, the diameter of each of the two smaller circles is the radius of the larger circle. If the two smaller circles have a combined area of square unit, then what is the area of the shaded region, in square units?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
If one of the smaller circles has radius , then its area is , and the area of the larger circle is = 4. Thus the area of the large circle is times the area of one of the small circles. So the area of the shaded region is equal to the combined area of the two smaller circles, which is square unit.
The ratio of the areas of two similar figures is the square of the ratio of their corresponding lengths. Because the diameter of the larger circle is twice the diameter of each smaller circle, it follows that the area of the larger circle is four times the area of each smaller circle. Therefore the shaded area is equal to the combined area of the two smaller circles.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions