¶ 2018 AMC8 Problem 19
Problem:
In a sign pyramid a cell gets a if the two cells below it have the same sign, and it gets a if the two cells below it have different signs. The diagram below illustrates a sign pyramid with four levels. How many possible ways are there to fill the four cells in the bottom row to produce a at the top of the pyramid?
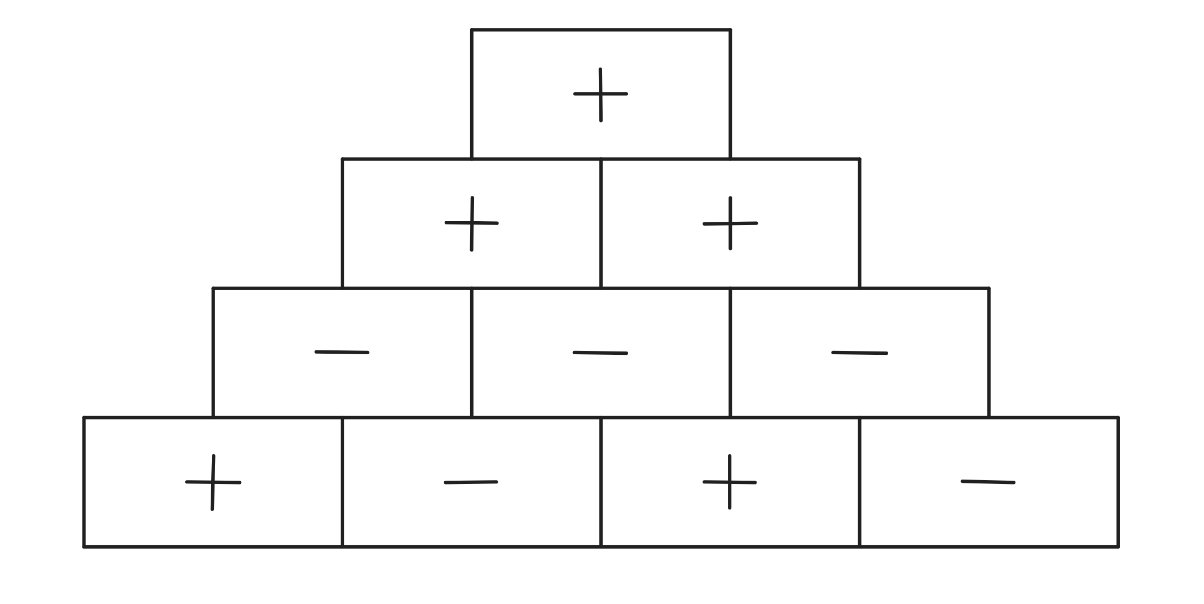
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Think of the sign as , and the sign as . Let a, b, c, and d denote the values of the four cells at the bottom of the pyramid, in that order. Then the cells in the second row from the bottom have values , and , and the cells in the row above this area = and = ( because doth and squared are .) Finally, the top cell has value . This value is if all four variables are or all four are , giving two ways; or, if two of the variables are and two are , giving 6 additional ways (,,,,, and ). Thus there are a total of 8 ways to fill the fourth row.
In order to produce a at the top of the pyramid, the second row must contain either or . Each leads to two possible arrangements for the third row. Consider the following cases.
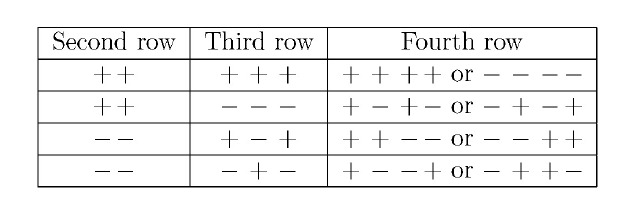
Thus, there are eight possible ways to fill the fourth row
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions