¶ 2018 AMC8 Problem 20
Problem:
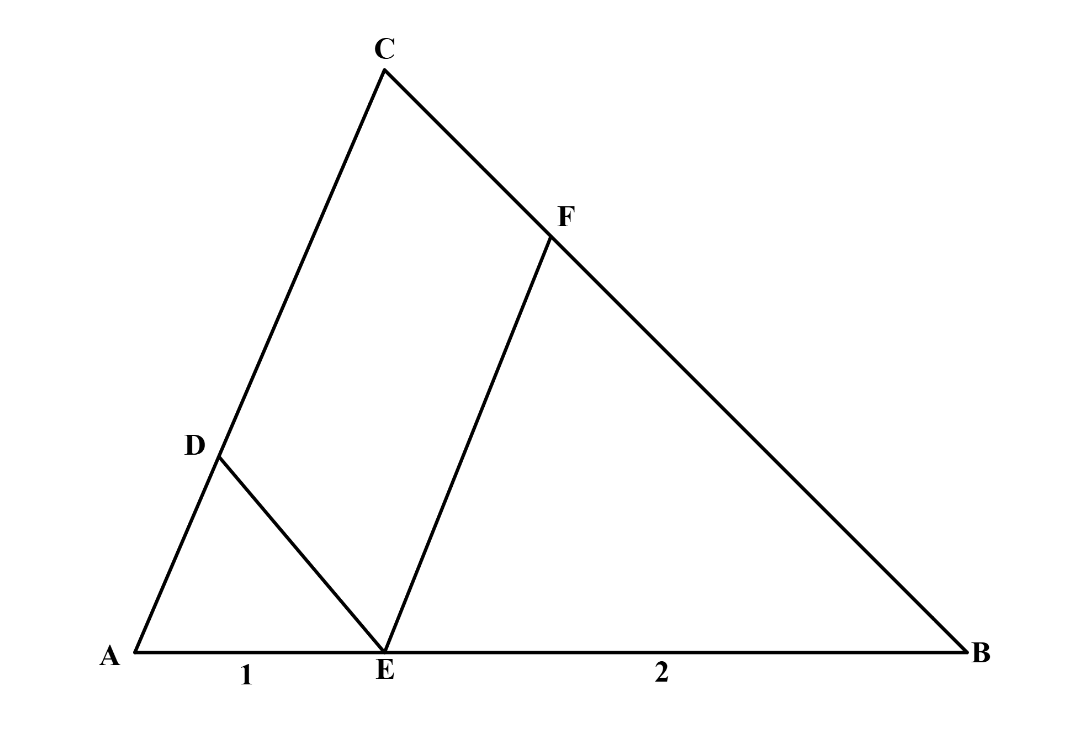
In , a point is on such that and . Point is on so that and point is on so that . What is the ratio of the area of to the area of triangle
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Triangles , and are similar with their sides in the ratio of . Therefore their areas are in the ratio of . The combined areas of and constitute of the area of , so the area of is of the area of .
Connecting corresponding points of trisection of the three sides of the triangle, as shown in the figure below, results in nine congruent triangles, four of which constitute .
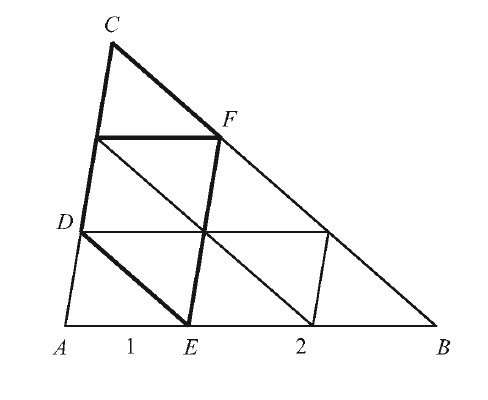
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions