Problem:
Point E is the midpoint of side CD in square ABCD, and BE meets diagonal AC at F. The area of quadrilateral AFED is 45. What is the area of ABCD?
Answer Choices:
A. 100
B. 108
C. 120
D. 135
E. 144
Solution:
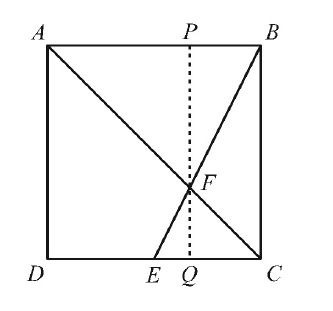
To see what fraction of the square is occupied by quadrilateral AFED, first note that △ADC occupies half of the area. Next note that because AB and CD are parallel, it follows that △ABF and △CEF are similar, and CE=21AB. Draw PQ through F such that PF and FQ are altitudes of △ABF and △CEF respectively. Then FQ = 21PF, So FQ=31PQ = 31BC. Therefore the area of △CEF is 21(CE)(FQ) = 21(21AB)(31BC) = 121(AB)(BC), which is 121 of the area of the square. Because the area of quadrilateral AFED equals the area of △ADC minus the area of △CEF, the fraction of the square occupied by quadrilateral AFED is 21−121=125. Because the area of AFED is 45, the area of ABCD is (512)(45)=108.
OR
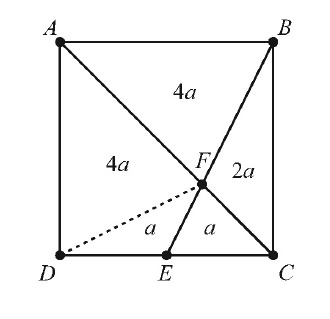
Let a denote the area of △CEF. Note that △ABF is similar to △CEF with ratio of similarity AB:CE=2:1. Therefore the area of △ABF is 4a. Because △DEF and △CEF have equal bases and have a common altitude from F, the area of △DEF is a. Because BF=2FE and because △CBF and △CEF have a common altitude from C, it follows that the area of △CBF is 2a. Similarly, △DAF has an area twice that of △DCF, so the area of △DAF is 4a. Finally, the area of quadrilateral AFED is 45=5a, so a=9 and therefore the area of square ABCD is 12a=108.
Answer: B.
The problems on this page are the property of the MAA's American Mathematics Competitions