¶ 2018 AMC8 Problem 24
Problem:
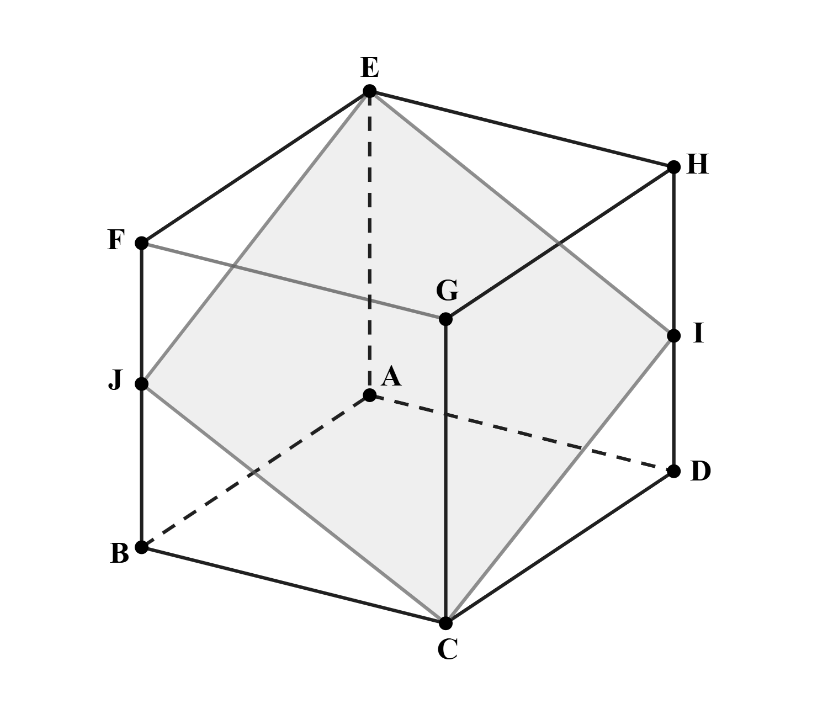
In the cube with opposite vertices and , and are the midpoints of segments and , respectively. Let be the ratio of the area of the cross-section to the area of one of the faces of the cube. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let denote the length of an edge of the cube. Now is a non-square rhombus whose area is , because the area of a rhombus is half the product of the lengths of its diagonals. By the Pythagorean Theorem, = = , and using the Pythagorean Theorem twice, = , Thus R = = = and .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions