¶ 2019 AMC8 Problem 12
Problem:
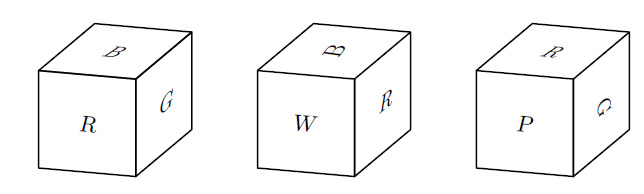
The faces of a cube are painted in six different colors: , , , , , and . Three views of the cube are shown below. What is the color of the face opposite the yellow face?
Answer Choices:
A. red
B. white
C. green
D. brown
E. purple
Solution:
The second view is a rotation of the first view on the axis through the brown face, implying that the green and white faces are opposite each other. The third view is a rotation of the first view on the axis through the green and white faces. Hence the purple face is opposite the brown face. Then the only face not seen is the aqua face, the back face in the first view and the bottom face in the third view. Thus the red face is opposite the aqua face.
Using the information from the diagrams in the problem, a net for the cube is shown in the following figure. The only face in the net not labeled must be aqua. Refolding the net to make a cube, the red face will be opposite the aqua face.
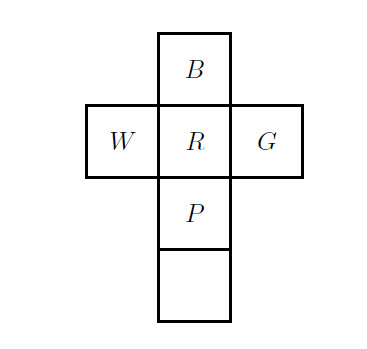
Using the information from the diagrams in the problem, there are four colors, brown, green,white, and purple, adjacent to the red face. The remaining color, aqua, must be opposite the
red face.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions