Problem:
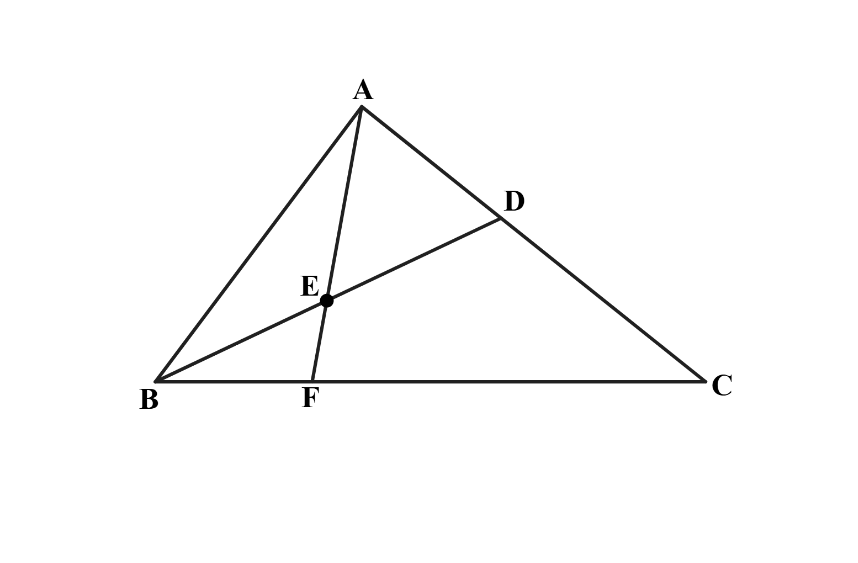
In triangle ABC, point D divides side AC such that AD:DC=1:2. Let E be the midpoint of BD and let F be the point of intersection of line BC and line AE. Given that the area of △ABC is 360, what is the area of triangle △EBF?
Answer Choices:
A. 24
B. 30
C. 32
D. 36
E. 40
Solution:
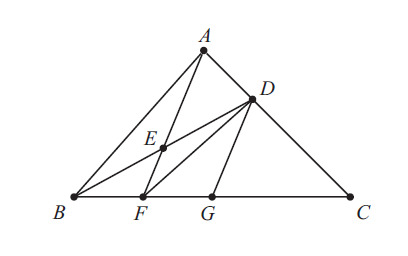
Let G be the point on side BC such that DG is parallel to AF . Then BF = FG because ΔBEF and ΔBDG are similar and BE=ED. Also 2FG=GC because ΔACF and ΔDCG are similar and $2AD = DC. Thus BC=BF+FG+GC=4BF . Let [XYZ] denote the area of a triangle XYZ. Then
[BDC]=32[BAC]=240
because DC=2AD and the triangles have the same altitude to line AC. Draw segment FD. Similarly, [BDF]=41[BDC]=60.Therefore[BEF]=21[BDF]=30.
OR
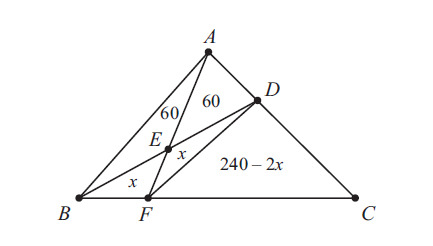
Because triangles ABD and DBC share the same altitude to line AC and AD:DC=1:2, the ratio of the areas [ABD]:[DBC] also is 1:2. Draw segment FD. Similarly the ratio [AFD] : [DFC] is 1 : 2.
Let x represent the area of ΔEBF. Then because BE=ED, the areas [ABE] and [AED] are equal and [EBF] = [DEF] = x.
Given that the area of ΔABC is 360, we can calculate the following areas:
[ABD]=31[ABC]=31(360)=120
[DBC]=32[ABC]=32(360)=240
[ABE]=[AED]=21[ABD]=21(120)=60
Then using the ratio of the areas of ΔAFD and ΔDFC we can solve for x.
[DFC][AFD]=21
[DBC]−[DBF][AED]+[DEF]=21
240−2x60+x=21
120+2x=240−2x
4x=120
x=30.
Therefore the area of ΔEBF is 30.
Answer: B.
The problems on this page are the property of the MAA's American Mathematics Competitions