¶ 2019 AMC8 Problem 25
Problem:
Alice has apples. In how many ways can she share them with Becky and Chris so that each of the three people has at least two apples?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Make a table of possibilities focusing on Alice.
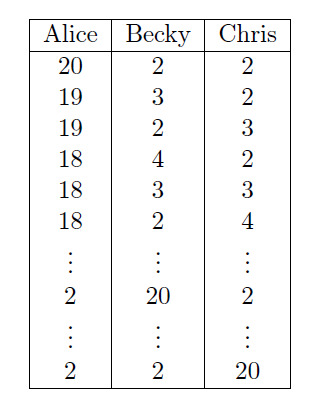
There are ways for Alice to share the apples.
Apply the sticks and stones counting method. Imagine stones in a row to represent the apples and sticks separating them.
To divide the apples into three groups, two of the sticks must be selected. The sticks at either end cannot be selected because each person must receive at least two apples. The number of ways to choose of the remaining sticks, denoted by , is . We also cannot select two adjacent sticks for the same reason. With the first and last sticks excluded, there are pairs of adjacent sticks. Therefore, there are ways to select the sticks and thereby distribute the apples.
Imagine first giving each of the girls two apples. Now there are apples remaining. Each way to distribute these apples among the three girls can be modeled by an arrangement of stones and sticks. For example,
corresponds to giving more apples to Alice, none to Becky, and more to Chris. The number of arrangements of stones and sticks is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions