¶ 2019 AMC8 Problem 5
Problem:
A tortoise challenges a hare to a race. The hare eagerly agrees and quickly runs ahead, leaving the slow-moving tortoise behind. Confident that he will win, the hare stops to take a nap. Meanwhile, the tortoise walks at a slow steady pace for the entire race. The hare awakes and runs to the finish line, only to find the tortoise already there. Which of the following graphs matches the description of the race, showing the distance traveled by the two animals over time from start to finish?
Answer Choices:
A.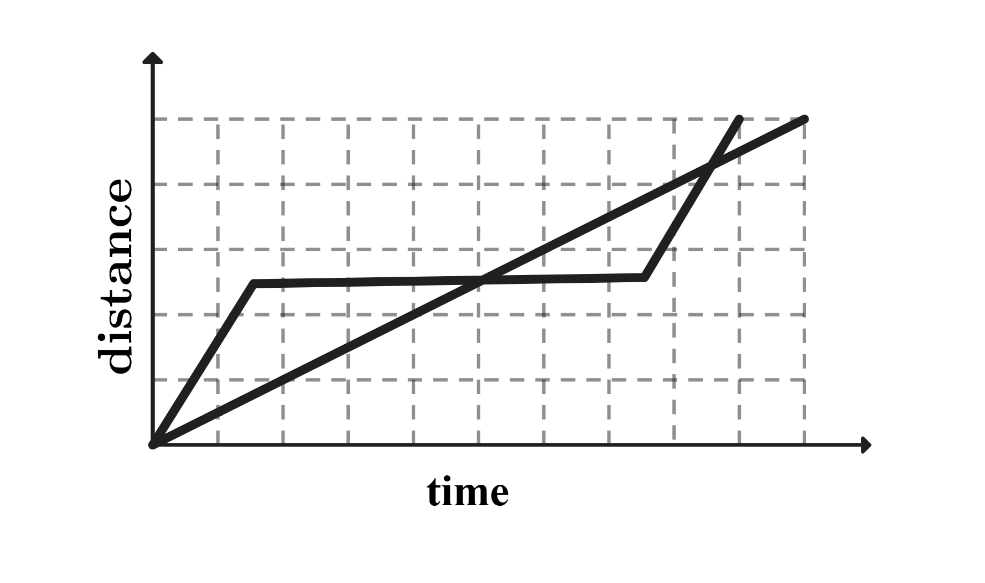 
B.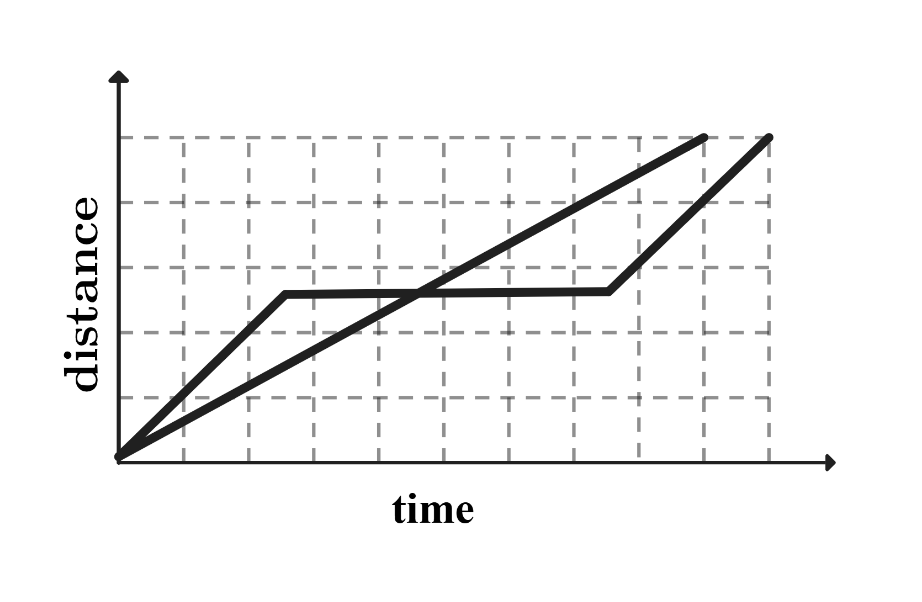 
C.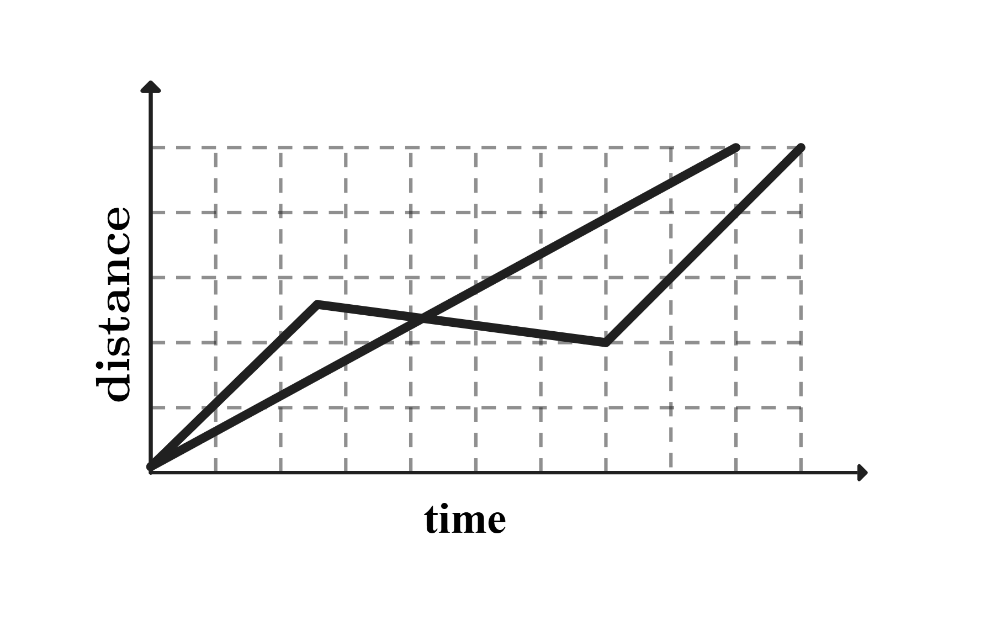 
D.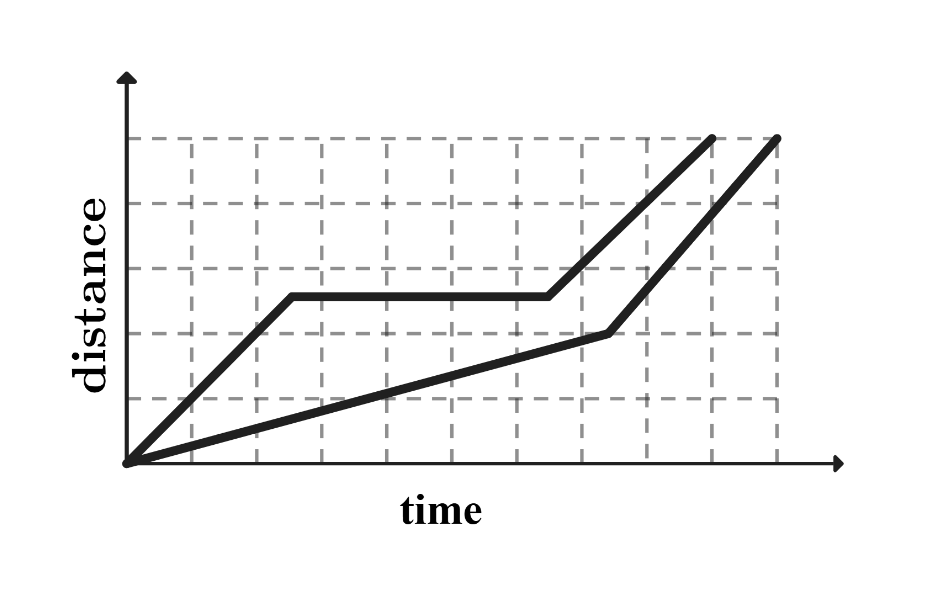 
E.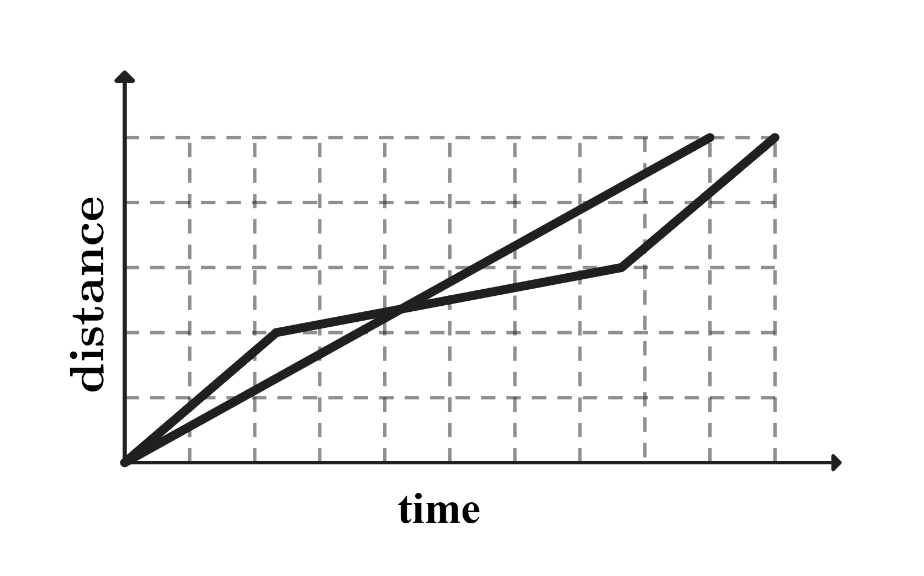 
Solution:
The tortoise moves at a slow and steady speed. The graph of the tortoise's journey corresponds to a straight line. Graph (D) is eliminated because there is no straight line. The hare's journey consists of running, then napping, then running again. The graph of
the hare's journey corresponds to a line with steeper slope than the tortoise's, a horizontal line during his nap when his distance does not change, and another steep line. Graphs (C) and (E) are eliminated because there is no horizontal line corresponding to the hare's nap. The tortoise reaches the finish line before the hare. Graph (A) is eliminated because it shows the hare catching up to the tortoise and finishing first. Only graph (B) matches the description of the problem.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions