¶ 2020 AMC8 Problem 18
Problem:
Rectangle is inscribed in a semicircle with diameter , as shown in the figure. Let and . What is the area of
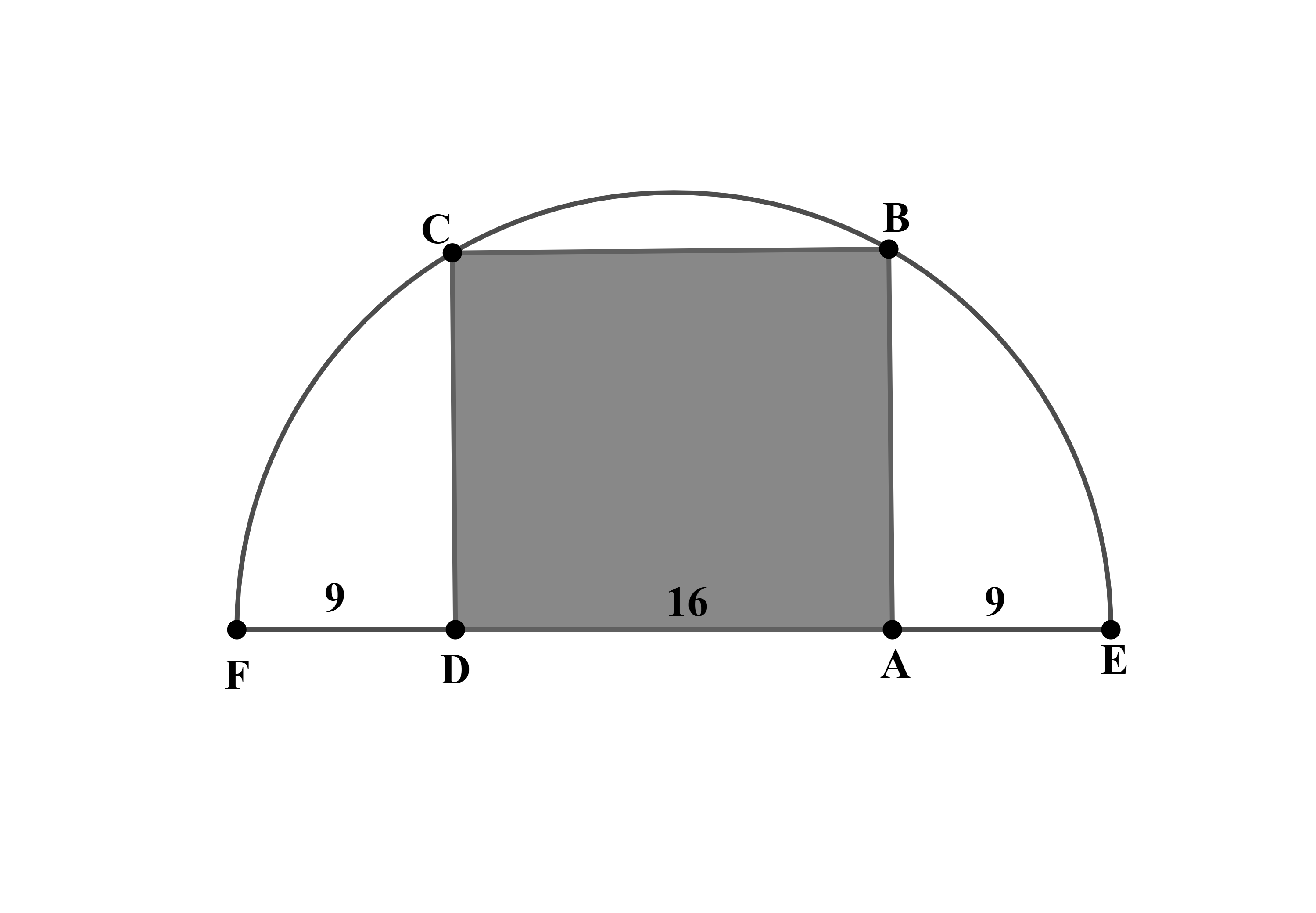
Answer Choices:
A.
B.
C.
D.
E.
Solution:
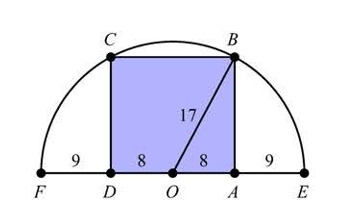
Let be the center of the circle. Then and radius . Draw radius which also has length . Then is a right triangle with hypotenuse and base leg . By the Pythagorean Theorem . The area of rectangle is = = .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions