¶ 2020 AMC8 Problem 21
Problem:
A game board consists of squares that alternate between blank and colored. The figure below shows square in the bottom row and square in the top row. A marker is placed at . A step consists of moving the marker onto one of the adjoining blank squares in the row above. How many -step paths are there from to
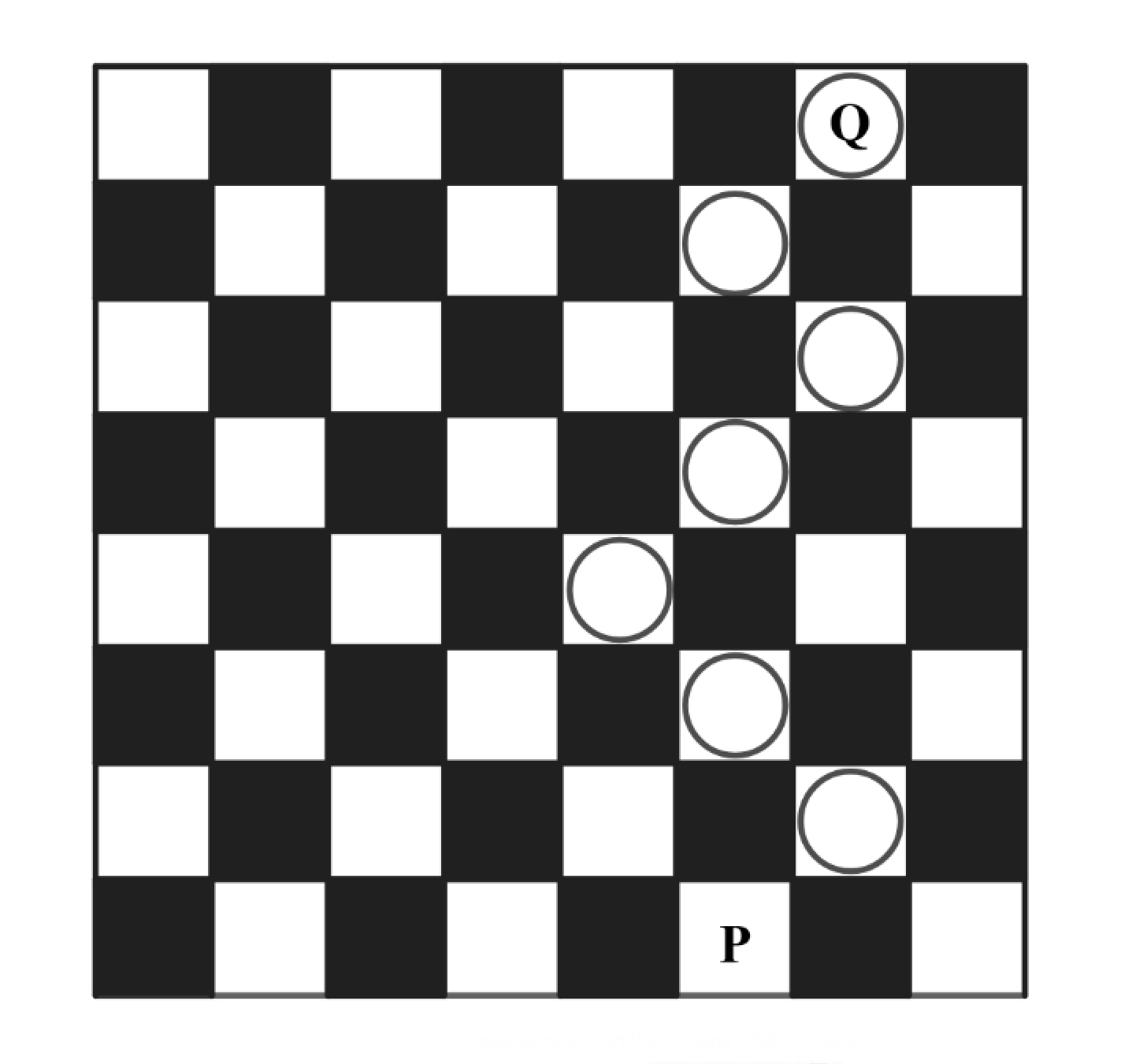
Answer Choices:
A.
B.
C.
D.
E.
Solution:
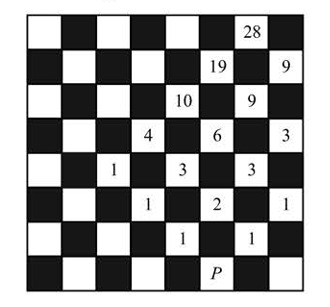
Beginning with the row above and filling in one row at a time, the number of paths that lead from to each square can be counted, as shown in the figure below. (Squares that cannot be reached or do not lead to in moves are left blank.) Note that the number of paths leading to a square equals the sum of the counts in the adjoining squares below it. (For example, to reach the square with paths, it is necessary to pass through one of the adjoining squares below; they have and paths leading to them, respectively.) Applying this counting method to each row, moving up from the bottom, results in a total of seven-step paths from to .
Each step moves the marker either one column to the left or one column to the right . Because is one column to the right of , each path must consist of moves to the right and moves to the left. Ignoring the possibility that a path may extend past the right edge of the board, the number of paths from to is equivalent to the number of distinguishable permutations of . which equals the number of combinations of objects taken at a time: .
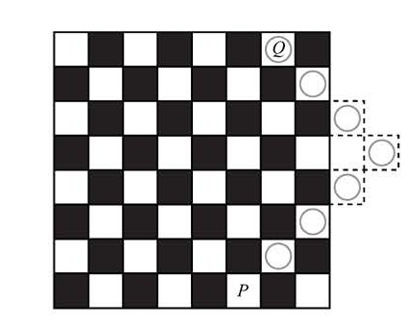
This total, however, includes paths that move the marker off the right edge of the board. One such path is shown below. path leaves the board when the number of moves exceeds the number of moves by . There are paths that extend beyond the board: . , , and the paths that begin with . Removing these paths leaves seven-step paths from to .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions