¶ 2020 AMC8 Problem 4
Problem:
Three hexagons of increasing size are shown below. Suppose the dot pattern continues so that each successive hexagon contains one more band of dots. How many dots are in the next hexagon?
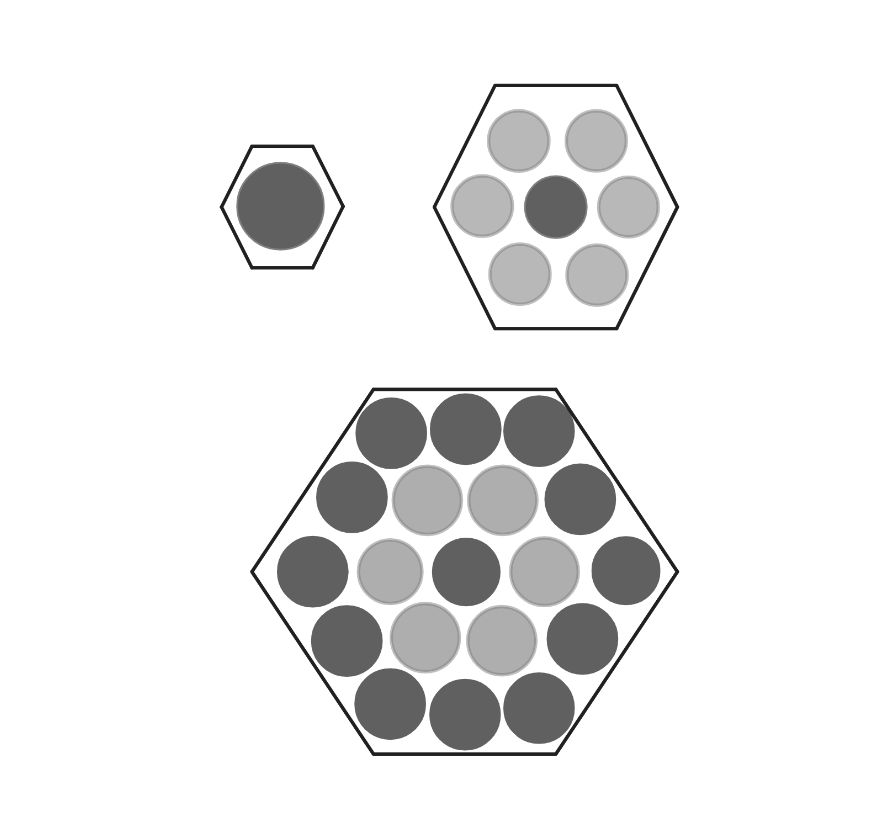
Answer Choices:
A.
B.
C.
D.
E.
Solution:
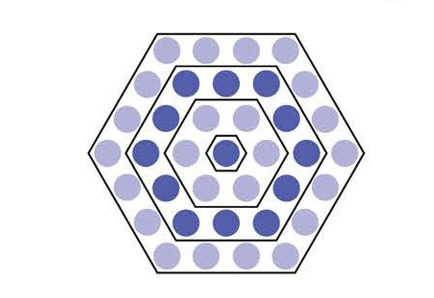
The fourth hexagon has bands of dots surrounding a center dot, as shown below. The innermost band has dots, the middle band has dots, and the outermost band has dots. Therefore the total number of dots in the fourth hexagon is
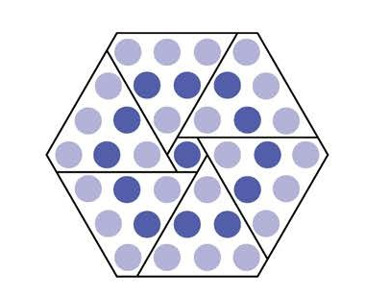
Excluding the center dot, each hexagon can be subdivided into six congruent triangular regions, as shown in the figure below. In the fourth hexagon, each triangular region contains dots, so the total number of dots in the fourth hexagon is .
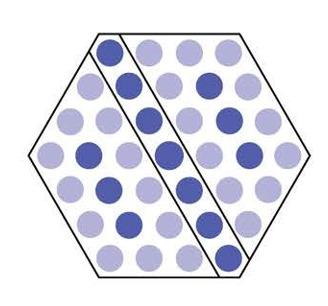
In each hexagon, the dots that lie on a diagonal form a line of symmetry, as shown in the figure below. The fourth hexagon has dots on a diagonal and dots on either side, for a total of dots.
: The number of dots in each hexagon is called a number. Generalizing from the first and second solutions, the number can be calculated as
Generalizing from the third solution, the nth hex number equals
It can be shown that the sum of the first in hex numbers is . For example, the sum of the first hex numbers is the sum of the first hex numbers is , and the sum of the first hex numbers is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions