¶ 2022 AMC8 Problem 20
Problem:
The grid below is to be filled with integers in such a way that the sum of the numbers in each row and the sum of the numbers in each column are the same. Four numbers are missing. The number in the lower left corner is larger than the other three missing numbers. What is the smallest possible value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let , and be the other missing numbers, as shown in the figure below.
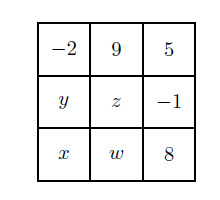
The sum of the numbers in each row and column is . It follows that , , , and . It is given that is larger then the other missing numbers. The sum equals , so . If , then the values , , and satisfy the requirements of the problem. Therefore is the smallest integer that can be placed in the lower left corner.
Let be the number in the lower left corner. The sum of the numbers in each row and column is , so the remaining entries can be expressed in terms of , as shown below.
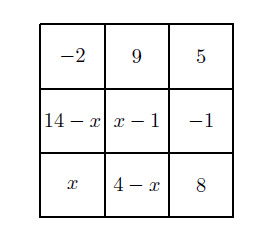
Note that it is always the case thta . This means that the only condition that must be satisfied is , which implies that , and hence . Therefore is the smallest integer that can be placed in the lower left corner.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions