¶ 2022 AMC8 Problem 21
¶ nan
Problem:
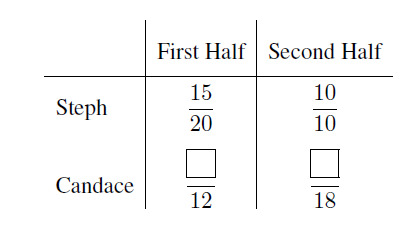
Steph scored baskets out of attempts in the first half of a game, and baskets out of attempts in the second half. Candace took attempts in the first half and attempts in the second. In each half, Steph scored a higher percentage of baskets than Candace. Surprisingly they ended with the same overall percentage of baskets scored. How many more baskets did Candace score in the second half than in the first?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Steph and Candace each had a total of attempts. Steph scored a total of baskets and the two players ended with the same percentage of baskets scored, so Candace also scored baskets. In the first half of the game, Steph was successful in of his attempts. Candace was less successful, so she scored fewer than of her attempts, making fewer than baskets. In the second half, Steph succeeded in all of his attempts, but Candace missed at least one of her shots, so she scored fewer than baskets. Because Candace ended with a total of baskets, she must have scored and baskets in the two halves, respectively, making more baskets in the second half.
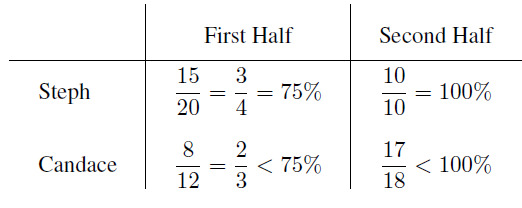
This result is an example of Simpson’s paradox. Although one player had a higher percentage score in each half, it was possible for the two players to end with the same overall percentage.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions