¶ 2022 AMC8 Problem 25
Problem:
A cricket randomly hops between leaves, on each turn hopping to one of the other leaves with equal probability. After hops, what is the probability that the cricket has returned to the leaf where it started?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Suppose the cricket starts at leaf . Consider the two -hop sequence patterns that start and end at shown below, with each blank representing a non- leaf. For each pattern, the number of sequences is listed. Note that there are ways to move from to a non- leaf, and there are ways to move from one non- leaf to another non- leaf.

In all there are possible -hop sequences starting at . The probability that the cricket is back at after hops is .
Suppose the cricket starts at leaf . Consider its position after hops and how it can return to on the hop. There are possible sequences of hops, and the only sequences that end at are those that visit two of the other leaves. There are choices for the first leaf and choices for the second leaf, so after hops, the cricket is at with probability , which implies that it is not at with probability . On the 4th hop the cricket cannot go from to , but it goes from any other leaf to S with probability . Therefore the cricket returns to after hops with probability .
Suppose the cricket starts at leaf . The number of ways to reach each leaf after each hop can be found by adding the counts at adjacent leaves.
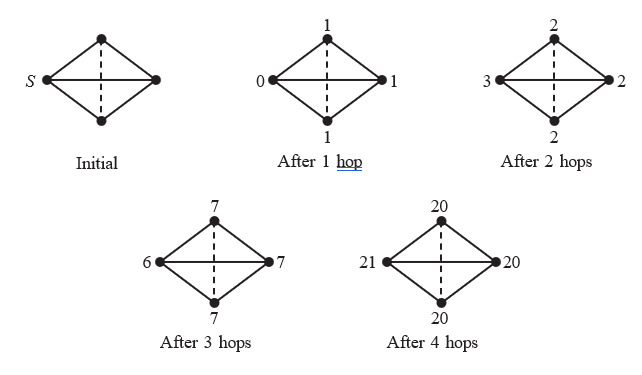
For example, there are ways to reach leaf in hops because there are ways to reach each of the leaves in hops. In all there are possible sequences of hops. The probability that the cricket is back at after hops is .
A recurrence relation can be used to solve this problem. Let and represent the probability that after hops the cricket is at or not at , respectively, with and . Then for , and . Applying this recurrence leads to the desired probability .
Answer: \boxed
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions