¶ 2022 AMC8 Problem 6
Problem:
Three positive integers are equally spaced on a number line. The middle number is and the largest number is times the smallest number. What is the smallest of these three numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let and represent the smallest and largest integers, respectively, with the number between them. The three integers are equally spaced, so and must be equidistant from . Because is greater than and is a multiple of , the smallest possible value of is and hence the smallest possible value of is . If and , the number a will be farther from than . The same is true if and . If and , however, both and will be units from . For larger values of , the number will be closer to than . Therefore and is the only solution, and is the smallest of the three numbers.
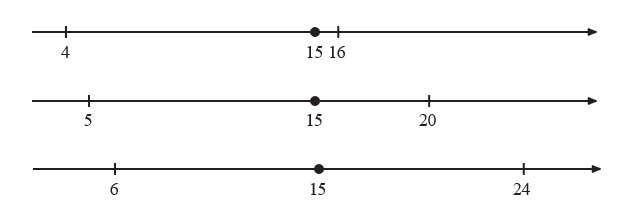
Let and represent the smallest and largest numbers, respectively. The distance between the smallest number and the middle number is . The distance between the largest number and the middle number is . The three integers are equally spaced, so the two distances must be equal. Therefore
The smallest number is .
Let denote the difference between the first two numbers. The three numbers are equally spaced, so the three numbers can be expressed as , , and . It is given that the largest number is four times the smallest, so
Solving for gives
Therefore the smallest number is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions