¶ 2023 AMC8 Problem 12
Problem:
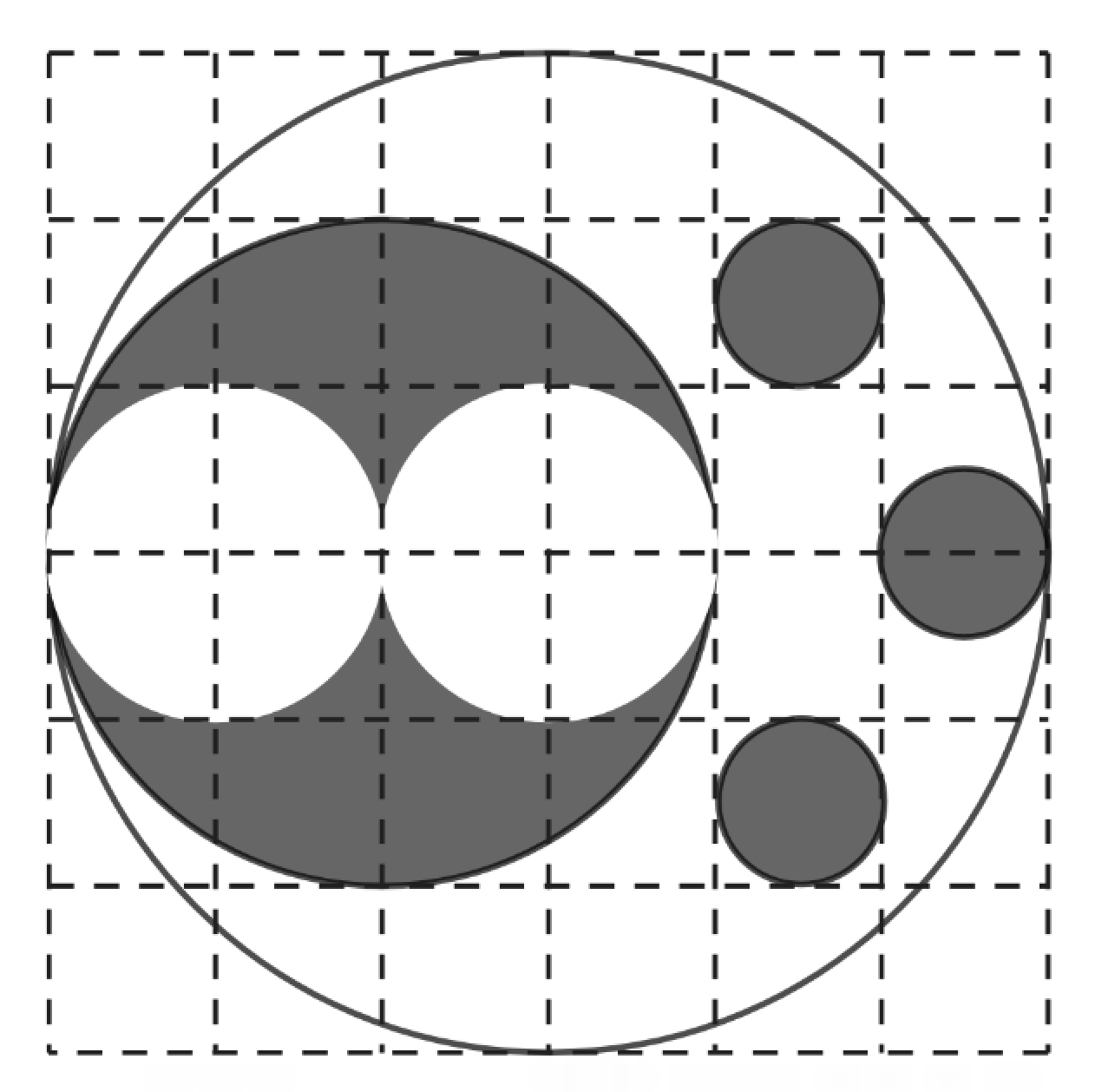
The figure below shows a large unshaded circle with a number of smaller unshaded and shaded circles in its interior. What fraction of the interior of the large unshaded circle is shaded?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The large white circle has a radius of units, so its area is square units.
There are three small shaded circles, each of which has a radius of unit. This means each small shaded circle has an area of square units. Together, they contribute square units of shaded area.
Finally, the larger shaded circle has a radius of units, so its area is square units, however it also contains two white circles. Each of those white circles has a radius of unit, so the white circles occupy square units.
In total the shaded area is square units. Therefore the fraction of the large white circle that is shaded is
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions