¶ 2023 AMC8 Problem 13
Problem:
Along the route of a bicycle race, water stations are evenly spaced between the start and finish lines, as shown in the figure below. There are also repair stations evenly spaced between the start and finish lines. The water station is located miles after the repair station. How long is the race in miles?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The repair stations are equally spaced along the route, so they divide the total race distance into thirds. Similarly, the water stations are equally spaced, so they divide the distance into eighths. The 1 repair station is of the way from start to finish, and the water station is miles further, of the distance along the way. The difference between and is , and because of the total distance is miles, the race must be miles long.
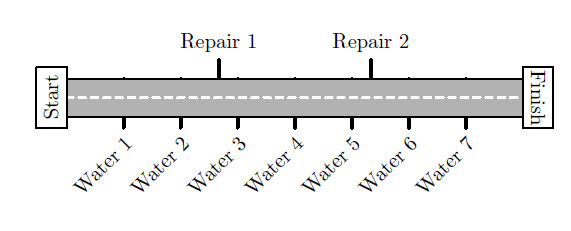
Let the total distance be miles. Then the water stations are spaced miles apart and the repair stations are miles apart. It is given that the water station is located miles after the repair station, so
Multiplying both sides of the equation by and simplifying gives
Therefore the length of the race is miles.
Let represent the distance between water stations and represent the distance between repair stations in miles. The stations are equally spaced along the road and the water station is located miles past the repair station, so
Solving for in the second equation gives and substituting into the first equation yields
thus
Therefore the length of the race is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions