¶ 2023 AMC8 Problem 16
Problem:
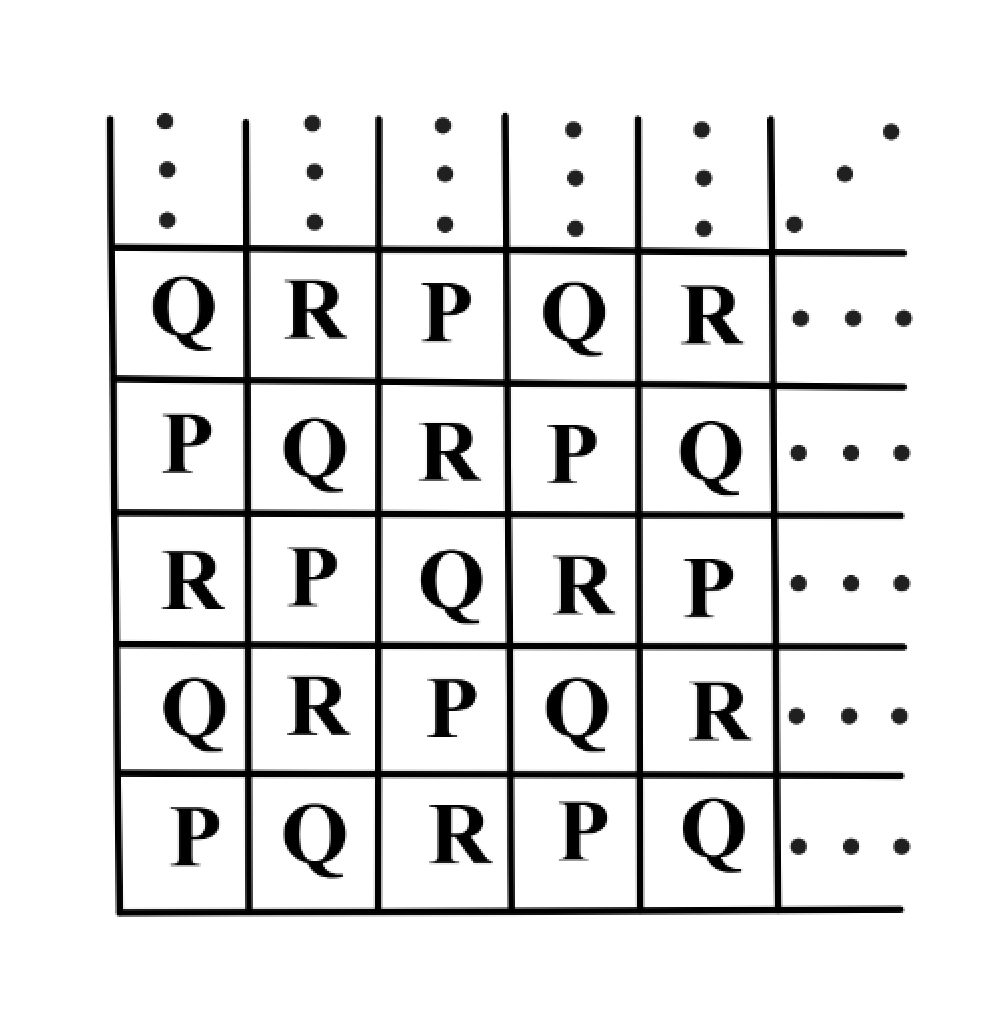
The letters , , and are entered into a table according to the pattern shown below. How many s, s, and s will appear in the completed table?
Answer Choices:
A. , ,
B. , ,
C. , ,
D. , ,
E. , ,
Solution:
A copy of the third column can be inserted into the table as the st column to form a larger table. Each row of the new table has Ps, Qs, and Rs. Because there are rows, the new table has a total of each of the Ps,Qs, and Rs. As there are Ps, Qs, and Rs in the st column, subtracting each from the total of leaves Ps, $ Qs, and Rs in the original table.
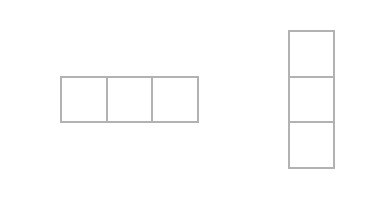
Consider covering the board with tiles called . A key realization is that any such triomino will cover exactly one P, one Q, and one R (in some order).
Divide the square into four regions—an square, a rectangle, an rectangle, and a square—as shown below (not to scale):
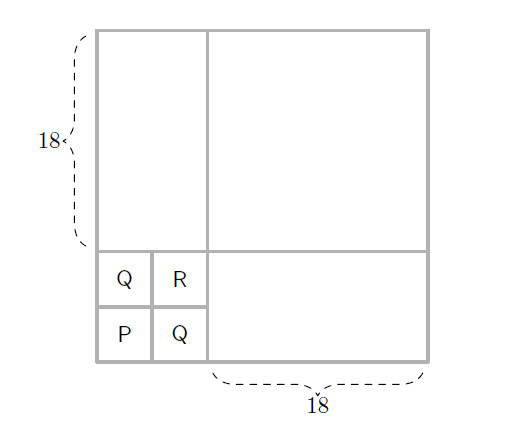
The two rectangles and the square each can be covered by non-overlapping triominoes because is divisible by . Hence these three regions contain equal numbers of Ps, Qs, and Rs. Observe that the lower left corner of the board contains one P, two Qs, and one R. Therefore the entire board will contain one more Q than it does Ps and Rs.
The board has cells, and gives a quotient of with a remainder of . That remainder accounts for the extra Q cell. Therefore there are Ps, Qs, and Rs in the completed table
The square can be broken into diagonals, each of which contains all Ps, all Qs, or all Rs. Starting in the lower left corner, there is a diagonal of 1 , then a diagonal of 2 Qs, then 3 Rs, 4 Ps, 5 Qs, and so on. The longest diagonal contain letters, after which the diagonal lengths decrease down to .
Let represent the number of Ps, represent the number of Qs, and r represent the number of Rs. Then , , and can be computed by summing the diagonal lengths:
The total must equal . Observe that and have the same summands, so their values are equal. Also observe that each of the first summands of is exactly more than the corresponding summand of , while each of the last summands of is exactly less than the corresponding summand of . The difference between the middle summands of and is , so the value of is exactly more than the value of . Therefore , so . The table contains 133 Ps, 134 Qs, and 133 Rs.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions