¶ 2023 AMC8 Problem 17
Problem:
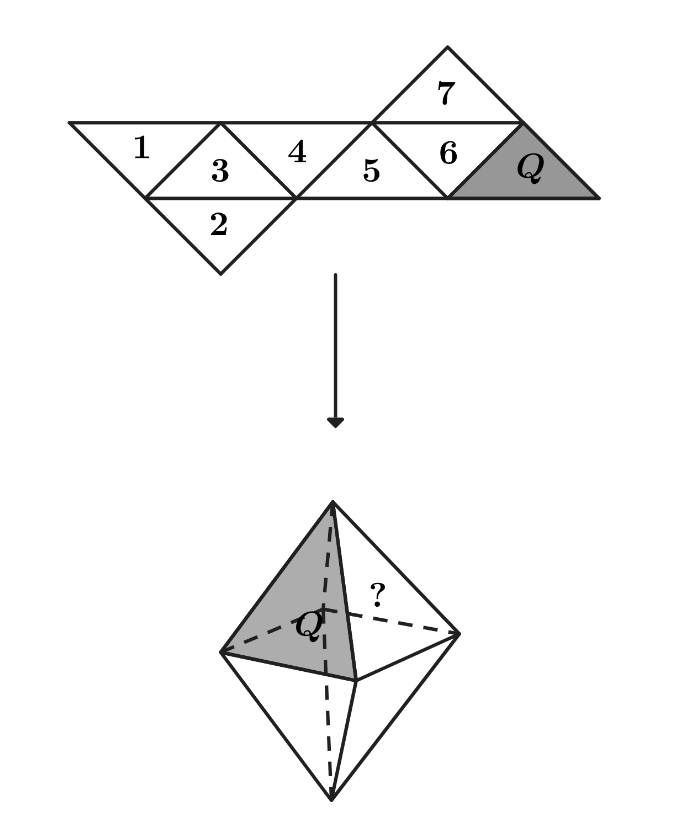
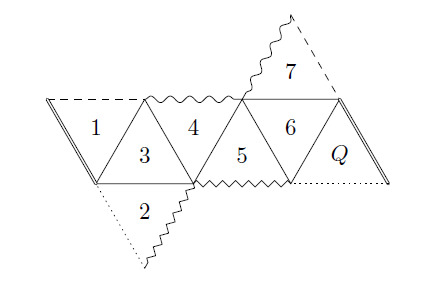
A regular octahedron has eight equilateral triangle face with four faces meeting at each vertex. Jun will make the regular octahedron shown in the figure by folding the piece of paper below. Which number face will end up to the right of the shaded region
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The left figure shows that the four faces in the top half of the octahedron must be , and the unknown face. Note that each vertex of the octahedron belongs to exactly four faces. The figure shows that the four faces , and all meet at a vertex. Since this vertex cannot be part of , or the unknown face, it is the vertex at the bottom of the octahedron and the faces , and are the four faces in the bottom half of the octahedron. By elimination, the remaining face is in the top half of the octahedron and must end up to the right of . The front and back views of the folded octahedron are shown below.
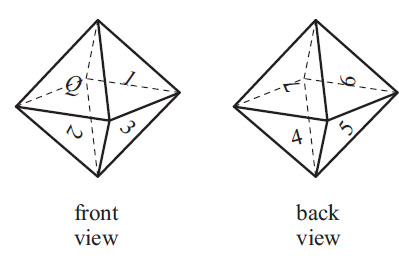
The top edge of face will meet the left edge of face , the top edge of face will meet the right edge of face , and the left edge of face will meet the right edge of , so face will end up to the right of .
To complete the octahedron, the right edge of face will meet the bottom edge of face , and the left edge of face will meet the bottom edge of .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions