¶ 2023 AMC8 Problem 18
Problem:
Greta Grasshopper sits on a long line of lily pads in a pond. From any lily pad, Greta can jump pads to the right or pads to the left. What is the fewest number of jumps Greta must make to reach the lily pad located pads to the right of her starting position?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Assume the lily pads are labeled as if they are on a number line, with Greta Grasshopper starting on pad and ending on pad .
First note that the order in which Greta makes her jumps does not affect her final destination. Only the number of jumps to the right or left matters. For example, jumping right, then left, then right, ends at pad , which is the same destination as jumping right twice, then left.
Therefore, it can be assumed that Greta takes some number of jumps to the right, followed by some number of jumps to the left. The jumps to the right must place Greta on a multiple of greater than , at a distance from that is a multiple of .
The first multiple of that is greater than is , but its distance from , which is , is not divisible by . The next multiple of is , but once again its distance from , wch is , is not divisible by . However, the next multiple of is and its distance from is , which is divisible by 3. Therefore, the shortest path to requires jumps to the right, followed by jumps to the left. This gives a minimum of jumps that Greta must make to reach the pad.
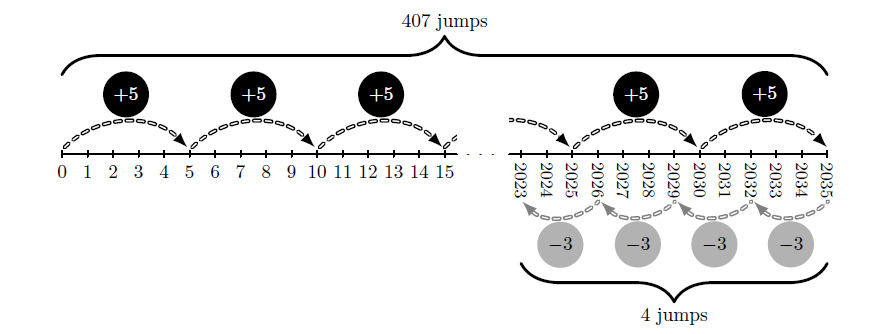
Let and represent the number of Greta’s jumps to the right and left, respectively. The goal is to minimize the sum given the condition . First check , which is the least value of that satisfies , placing Greta to the right of the lily pad. That value of does not lead to an integer value for , and neither does . The next value, , corresponds to the integer value , so the fewest number of jumps Greta must make to reach the pad is .
To reach the lily pad using the fewest number of jumps, Greta will make more right jumps than left jumps. Suppose each left jump is paired with a right jump, producing pairs, leaving unpaired right jumps. Then the total number of jumps is .
Each right jump will move pads to the right and each left-right pair of jumps will move pads to the right. It follows that solving the equation using the least value of P will minimize the total number of jumps.
Given that the quantity is a multiple of , the least possible value of is . The corresponding value of is . Therefore the fewest number of jumps Greta must make to reach the pad is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions