¶ 2023 AMC8 Problem 19
Problem:
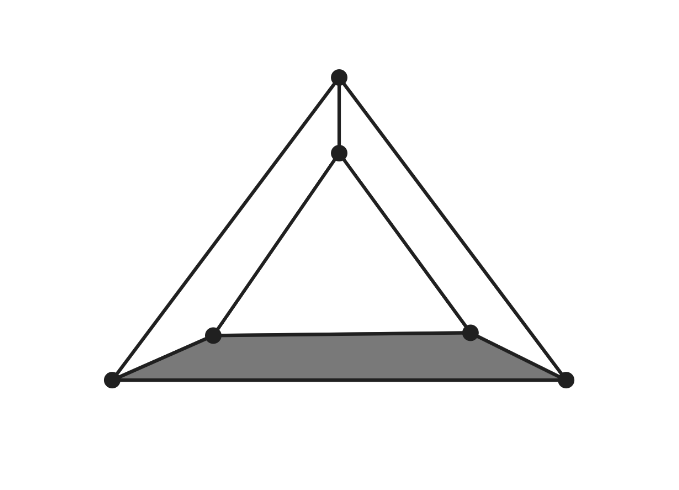
An equilateral triangle is placed inside a larger equilateral triangle so that the region between them can be divided into three congruent trapezoids, as shown below. The side length of the inner triangle is the side length of the larger triangle. What is the ratio of the area of one trapezoid to the area of the inner triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let the area of the inner triangle equal . Because the ratio of the triangle side lengths is , the ratio of their areas is . It follows that the area of the outer triangle is , and the area of the region between the triangles is . Each trapezoid has area equal to one third of the region: . Thus the ratio of the area of one trapezoid to the area of the inner triangle is , which equals .
Let be the area of the inner triangle. Because the ratio of the outer triangle side length to the inner triangle side length is , the ratio of their areas is . Thus the area of the outer triangle is . Let be the area of a trapezoid. Then
which simplifies to
yielding the proportion
Therefore the ratio of the area of one trapezoid to the area of the inner triangle is .
Shown below is an enlarged view of the shaded trapezoid.
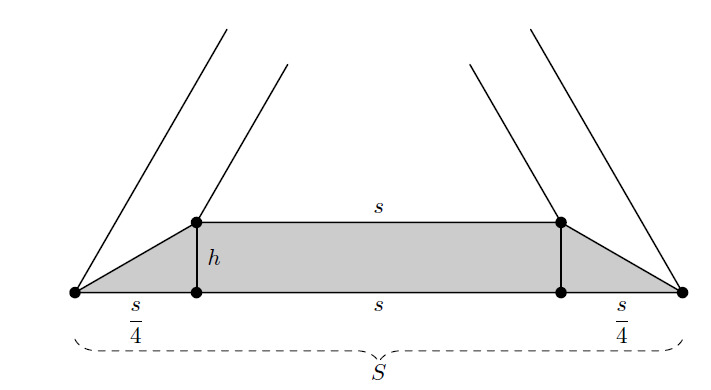
Let and denote the side lengths of the inner and outer triangles, respectively. The ratio of the two side lengths is , so . The area of the inner equilateral triangle equals half its base times its height.
The area of the shaded trapezoid equals its height times the average of its bases.
Note that the base angles of the trapezoid measure . Perpendiculars drawn from the base vertices of the inner triangle to the base of the trapezoid will form triangles.Each triangle has a base length of and a height . Thus the area of the trapezoid is
Dividing by gives
Therefore the ratio of the area of the trapezoid to the area of the inner triangle is .
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions