¶ 2023 AMC8 Problem 23
Problem:
Each square in a grid is randomly filled with one of the four gray-and-white tiles shown below on the right.
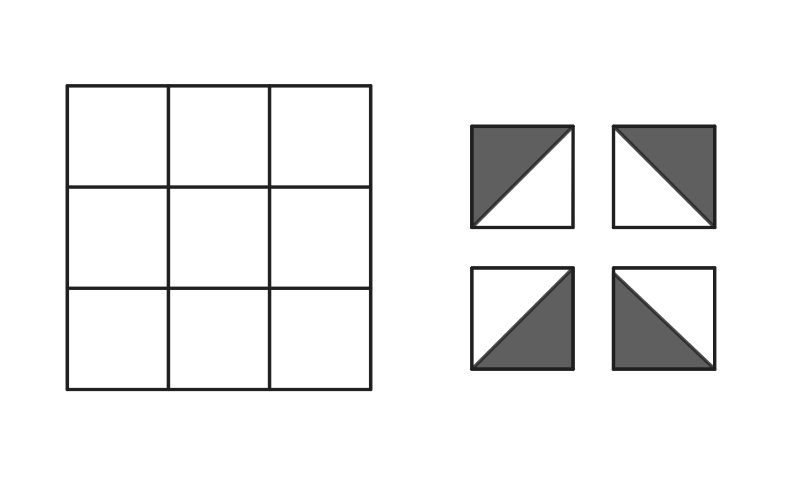
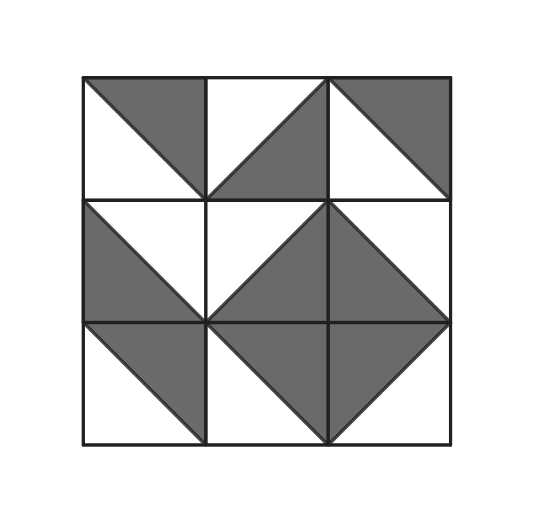
What is the probability that the tiling will contain a large gray diamond in one of the smaller grids? Below is an example of such tiling.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Observe that at most one large gray diamond can appear in a tiling. Because each of the squares is filled with of possible tiles, a total of tilings are possible. If a tiling has a gray diamond , then there are possible locations for the center of the diamond: any one of the corners of the center square. Once that location is determined, each of the remaining squares can be filled with any of the possible tiles, for a total of tilings. Therefore the probability that a tiling contains a gray diamond is
If a tiling has a gray diamond the diamond must include the center tile, which will have one corner that is all gray. The tiles adjacent to that corner must be oriented to match the gray color of the center tile. There is no restriction on the orientations of the other squares. Because each of the adjacent tiles has a probability of of having the correct orientation, the probability that a tiling g contains a large gray diamond is .
NOTE : These tiles are called , named after Sébastien Truchet (1657–1729), who studied the possible patterns formed by these tiles. Below are some of the patterns that can be made on a grid.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions