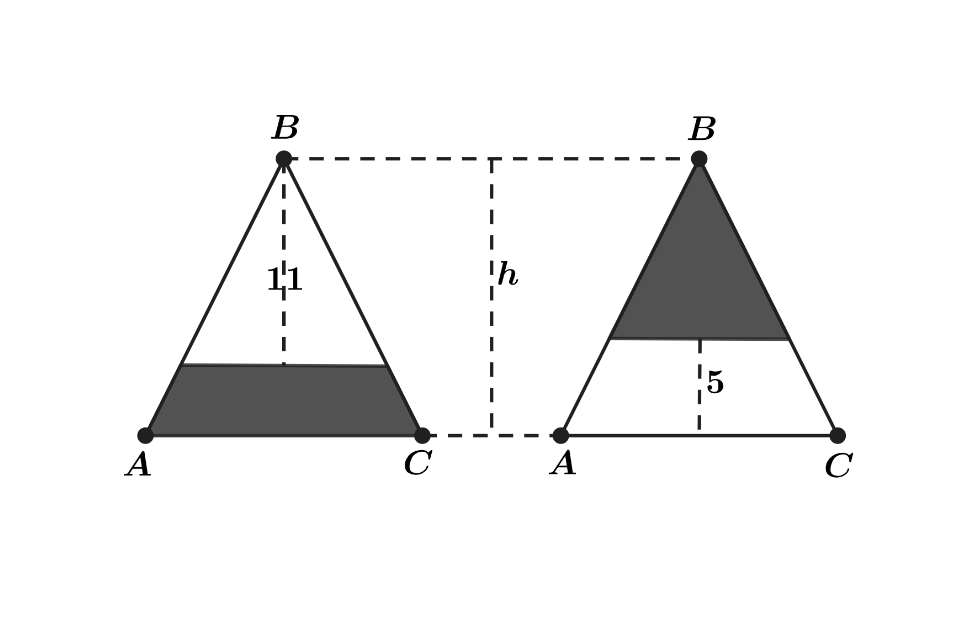
Problem:
Isosceles triangle △ABC has equal side lengths AB and BC. In the figures below, segments are drawn parallel to AC so that the shaded portions of △ABC have the same area. The heights of the two unshaded portions are 11 and 5 units, respectively. What is the height h of △ABC?
Answer Choices:
A. 14.6
B. 14.8
C. 15
D. 15.2
E. 15.4
Solution:
Given two similar triangles, the ratio of their areas is equal to the square of the ratio of their corresponding heights. Thus, in the figure on the left, the ratio of the areas of the unshaded triangle and △ABC is h2112. It follows that the fraction of △ABC that is shaded is 1−h2112 .
Similarly, in the figure on the right, the shaded triangle has height h−5, and fills h2(h−5)2 of △ABC. C. The shaded portions in the two figures are equal in area, so
1−h2112=h2(h−5)2
Multiplying both sides by h2 and expanding the right side gives
h2−112=h2−10h+25.
which simplifies to
10h=121+25=146h=10146=14.6.
Therefore the height h of △ABC is 14.6.
OR
Let the base of △ABC be b=AC. Then the area of the triangle is K=21bh.
In the left figure, let the upper triangle have a base of b1 and an area of K1=21⋅11⋅b1.
The upper triangle is similar to △ABC because their bases are parallel, so b111=bh and b1=11hb. Thus K1=2112hb.
In the right figure, the height of the upper triangle is h−5. Let its base be b2 and its area be K2=21b2(h−5). The upper triangle is similar to △ABC, so b2h−5=bh and b2=(h−5)hb. Thus K2=2(h−5)2hb.
The two shaded areas are equal.
K−K1=K221bh−2112hb=2(h−5)2hb
The equation above can be solved for h by first multiplying both sides of the equation by b2h, eliminating b.
h2−112=(h−5)2
Then expanding the expressions and simplifying gives
h2−121=h2−10h+2510h=146h=14.6
The height h of △ABC equals 14A6.
Answer: A.
The problems on this page are the property of the MAA's American Mathematics Competitions