¶ 2023 AMC8 Problem 4
Problem:
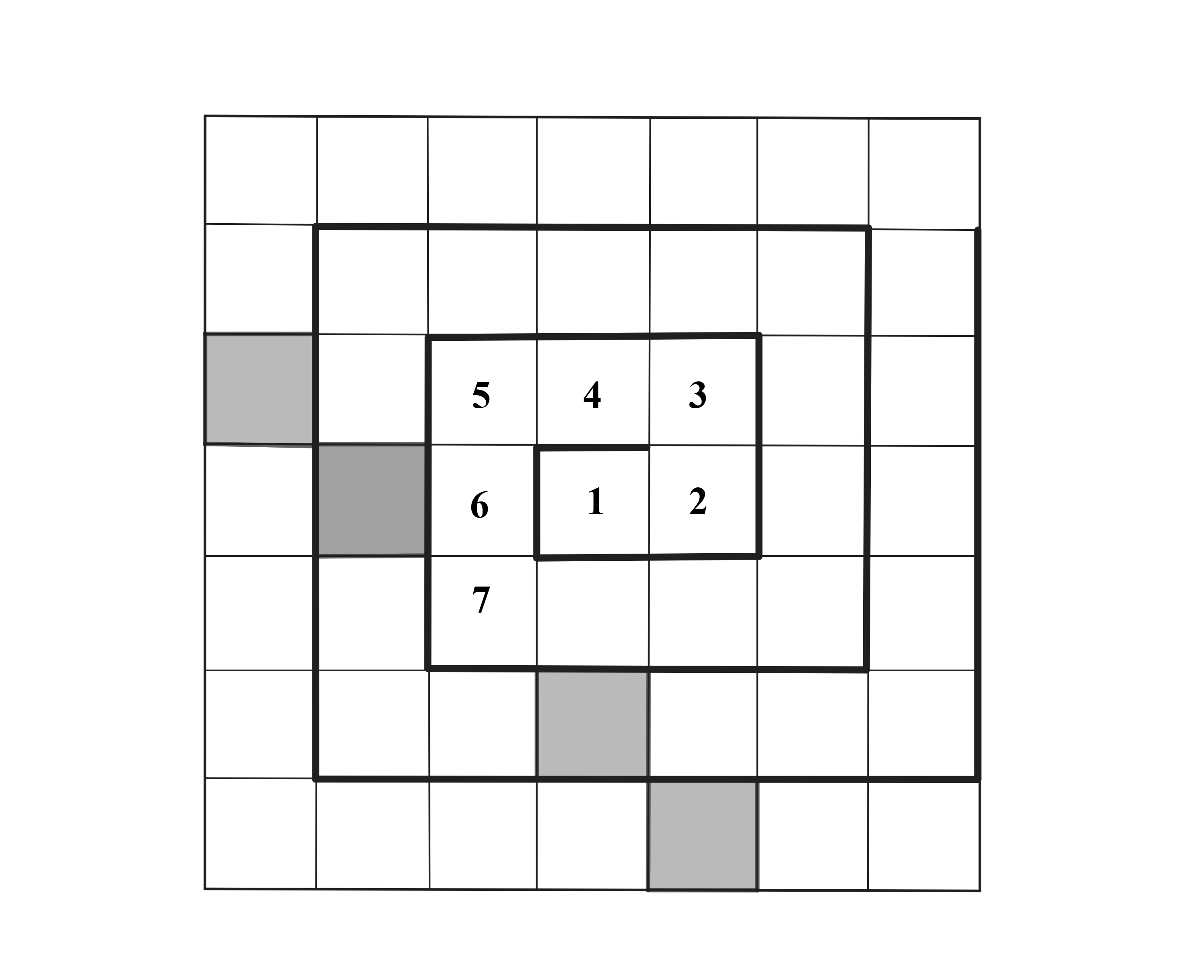
The numbers from to are arranged in a spiral pattern on a square grid, beginning at the center. The first few numbers have been entered into the grid below. Consider the four numbers that will appear in the shaded squares, on the same diagonal as the number . How many of these four numbers are prime?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
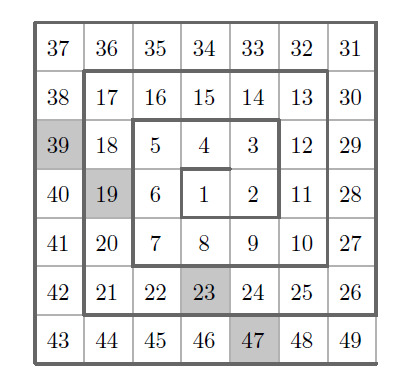
If the remaining numbers are entered into the grid using the spiral pattern, the shaded squares will correspond to the numbers , and . Of the four numbers, is the only composite, so of the numbers in the shaded squares are prime.
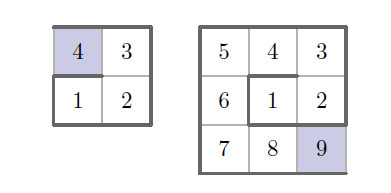
It is possible to determine the number in any square without filling in the entire grid by using the square numbers as reference points. Note that when the positive integers are arranged in a spiral pattern on an grid, the greatest number, , will appear either in the upper left corner (if is even) or in the lower right corner (if is odd), as shown below for and .
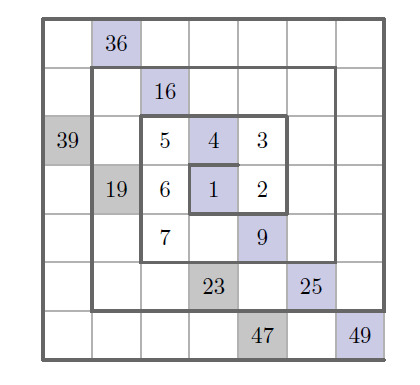
If the remaining square numbers are entered into the grid, one can determine that the shaded squares correspond to the numbers . Of the four numbers, is the only composite, so of the numbers in the shaded squares are prime.
This , or , is named after Stanislaw Ulam , who discovered that when the positive integers are arranged in this pattern, the prime numbers often fall along diagonal lines. These diagonal patterns can be seen in the figure below, which shows the prime numbers between and as black dots.

Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions