¶ 2023 AMC8 Problem 7
Problem:
A rectangle, with sides parallel to the -axis and -axis, has opposite vertices located at and . A line is drawn through points and . Another line is drawn through points and . How many points on the rectangle lie on at least one of the two lines?
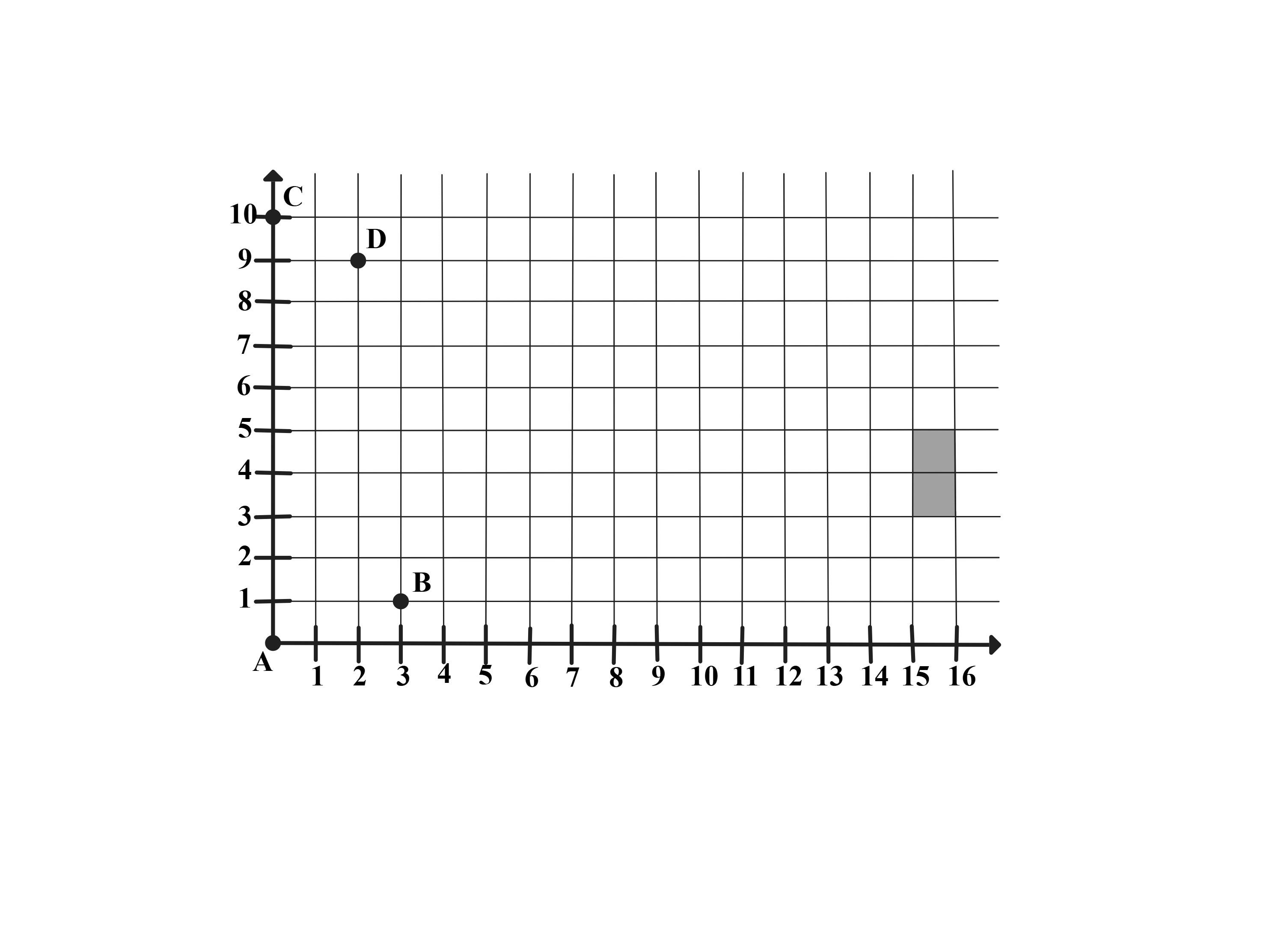
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Line has a slope of , moving up unit for every units to the right. It intersects the upper-left corner of the rectangle at . Line has a slope of , moving down unit for every units to the right. It passes through the points and , below the rectangle. Therefore is the only point on the rectangle that lies on the lines.
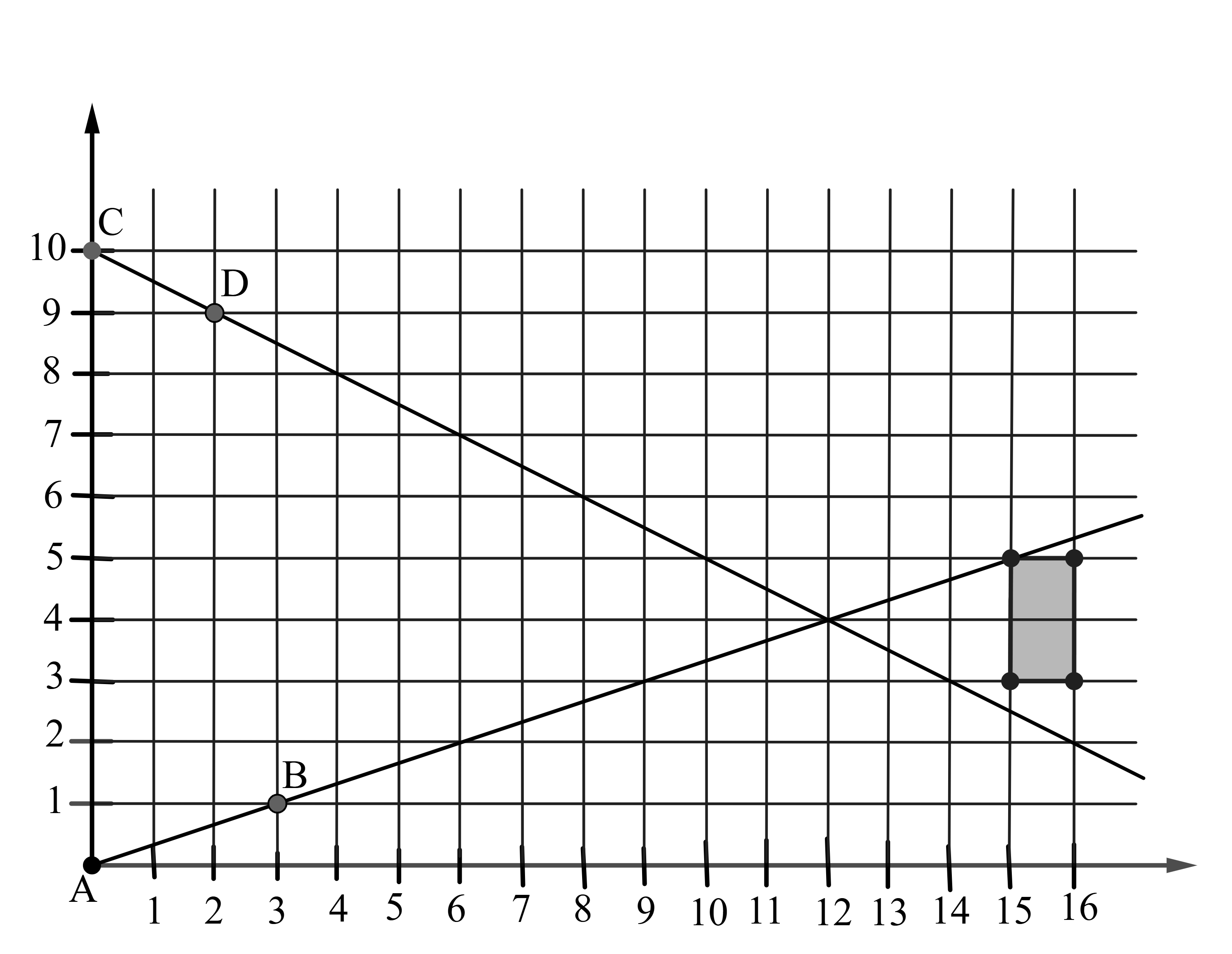
Line has the equation . It intersects the upper-left corner of the rectangle at . Line has the equation , which passes through the point , below the rectangle. Therefore is the only point on the rectangle that lies on the lines.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions