¶ 2026 AMC8 Problem 11
Problem:
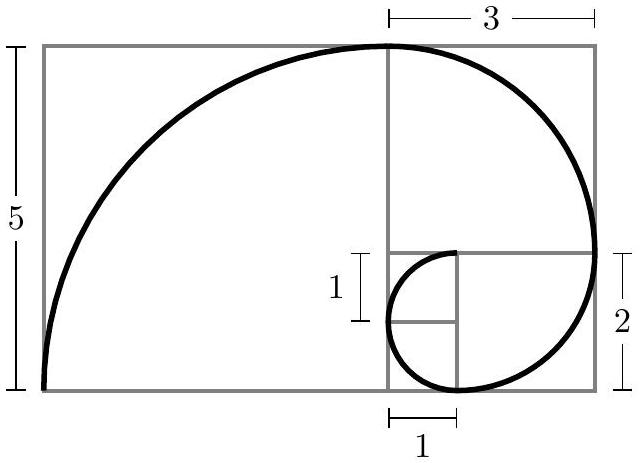
Squares of side length , , , , and are arranged to form the rectangle shown below. A curve is drawn by inscribing a quarter circle in each square and joining the quarter circles in order, from shortest to longest. What is the length of the curve?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
First, we look at the largest square to the right. The side length is . Since this is a quarter circle, we note that the radius of each circle is congruent to the side length of that specific square.
The circumference of a quarter circle (excluding the radii) is .
Largest square (side length ): The curve in this square is
Second square (side length ): The curve in this square is
Third square (side length ): The curve in this square is
Fourth and fifth square (side length ): The curve in each of these squares is
The total length is:
The problems on this page are the property of the MAA's American Mathematics Competitions