¶ 2026 AMC8 Problem 12
Problem:
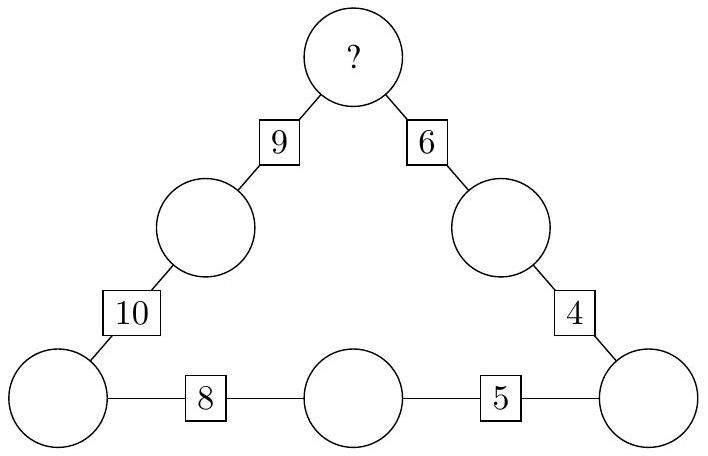
In the figure below, each circle will be filled with a digit from to . Each digit must appear exactly once. The sum of the digits in neighboring circles is shown in the box between them. What digit must be placed in the top circle?
Answer Choices:
A.
B.
C.
D.
E. it is impossible to fill the circles
Solution:
Note that in the very right, the corner circle must be either a or . To get a sum of in the middle of that side, you must have a number smaller than ; or . Because we cannot repeat digits, we cannot have two , a . Therefore, we have two cases, the right, corner circle being either a or .
Case 1: Right corner circle is
Immediately to the left of the is , meaning the circle in the middle bottom is . We see this leads to a problem, as continuing further left is an . To make the sum an , the left corner must also be a , which is not allowed due to no duplicates.
Case 2: Right corner circle is
Immediately to the left of the is , meaning the circle in the middle bottom is . This is valid, continuing down to the left, corner circle has to be . Going up, the left side, middle circle is a . The very top circle, the question mark must therefore be a , as the sum is . Continuing back down on the right, the middle circle must be a , which checks out with the sum of . This case is valid, and the final answer is .
The problems on this page are the property of the MAA's American Mathematics Competitions