¶ 2026 AMC8 Problem 13
Problem:
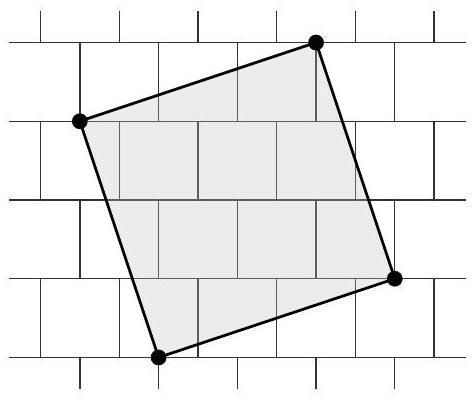
The figure below shows a tiling of unit squares. Each row of unit squares is shifted horizontally by half a unit relative to the row above it. A shaded square is drawn on top of the tiling. Each vertex of the shaded square is a vertex of one of the unit squares. In square units, what is the area of the shaded square?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Looking at the very top of the square, the side length with vertices at the highest -coordinate values is a length, we note, that is the simplest to measure. Visualizing a right triangle connecting those two vertices, the difference in the vertices' -coordinates is just units. The difference in the -coordinates is unit. By the Pythagorean Theorem, . We have that . Note that because is the side length, the area of the square is . Therefore, the area of the square is .
The problems on this page are the property of the MAA's American Mathematics Competitions