¶ 2026 AMC8 Problem 15
Problem:
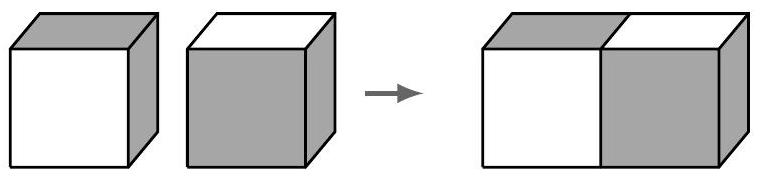
Elijah has a large collection of identical wooden cubes which are white on faces and gray on faces that share an edge. He glues some cubes together face-to-face. The figure below shows cubes being glued together, leaving gray faces visible. What is the fewest number of cubes that he could glue together to ensure that no gray faces are visible, no matter how he rotates the figure?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
For clear terminology, throughout this question, when referring to -axis, we mean left to right. -axis is front and back. -axis refers to up and down.
Our first observation is that when there are two gray faces of two separate cubes that are glued together, face to face, then there is at least one configuration that allows the other two respective gray faces to be attached by an edge. For example, after rotating the first cube one face by degrees counterclockwise on the plane and then rotating the cube one face degrees to the right on the -axis, we can glue the first and second to obtain a rectangular prism with a full gray rectangle on the right, and two gray faces covered, glued together to each other.
Notice now, if we duplicate this rectangular prism, and glue the two gray faces together, all the gray faces are hidden, covered by each other, and we therefore, have used boxes.
The problems on this page are the property of the MAA's American Mathematics Competitions