¶ 2026 AMC8 Problem 21
Problem:
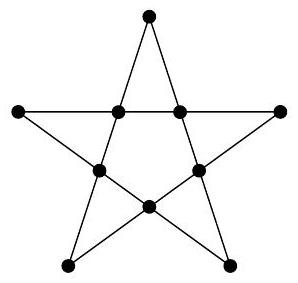
Charlotte the spider is walking along a web shaped like a -pointed star, shown in the figure below. The web has outer points and inner points. Each time Charlotte reaches a point, she randomly chooses a neighboring point and moves to that point. Charlotte starts at one of the outer points and makes moves (re-visiting points is allowed). What is the probability she is now at one of the outer points of the star?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
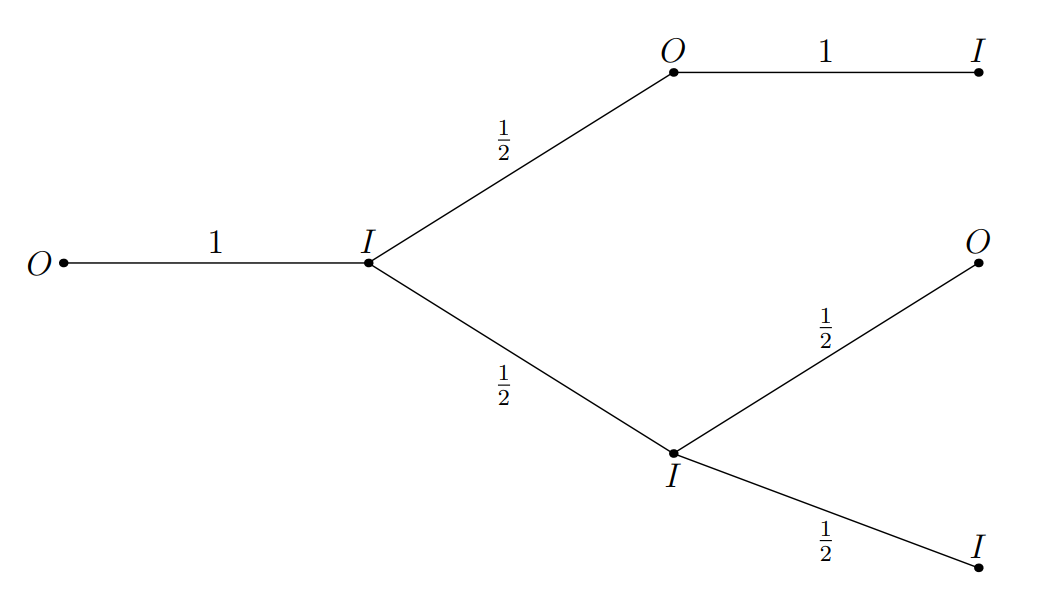
We can solve this problem by looking at a decision tree. We don't care which inner or outer point Charlotte the spider is currently on, since they are all connected to the same number of inner and outer points. Every outer point is connected to two inner points, and every inner point is connected to two outer points and two inner points. So we can trace the tree starting from an outer point.
From the outer point, there's a chance that the spider moves to an inner point. From the inner point, there's a chance of going to another inner point and a chance of going to an outer point. From there, the tree branches one more time in the same fashion as the spider takes its third step.
From all the possible endpoints, we can see that only one branch ends at an outer point. So we multiply the probabilities along the path from the starting outer point to the ending outer point and get our final probability: .
The problems on this page are the property of the MAA's American Mathematics Competitions