Problem:
Lakshmi has 5 round coins of diameter 4 centimeters. She arranges the coins in 2 rows on a table top, as shown below, and wraps an elastic band tightly around them. In centimeters, what will be the length of the band?
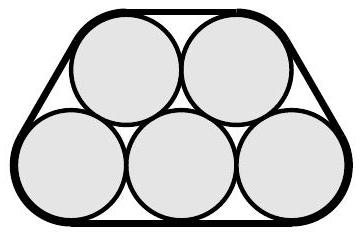
Answer Choices:
A. 2Ο+20
B. 25βΟ+20
C. 4Ο+20
D. 29βΟ+20
E. 5Ο+20
Solution:
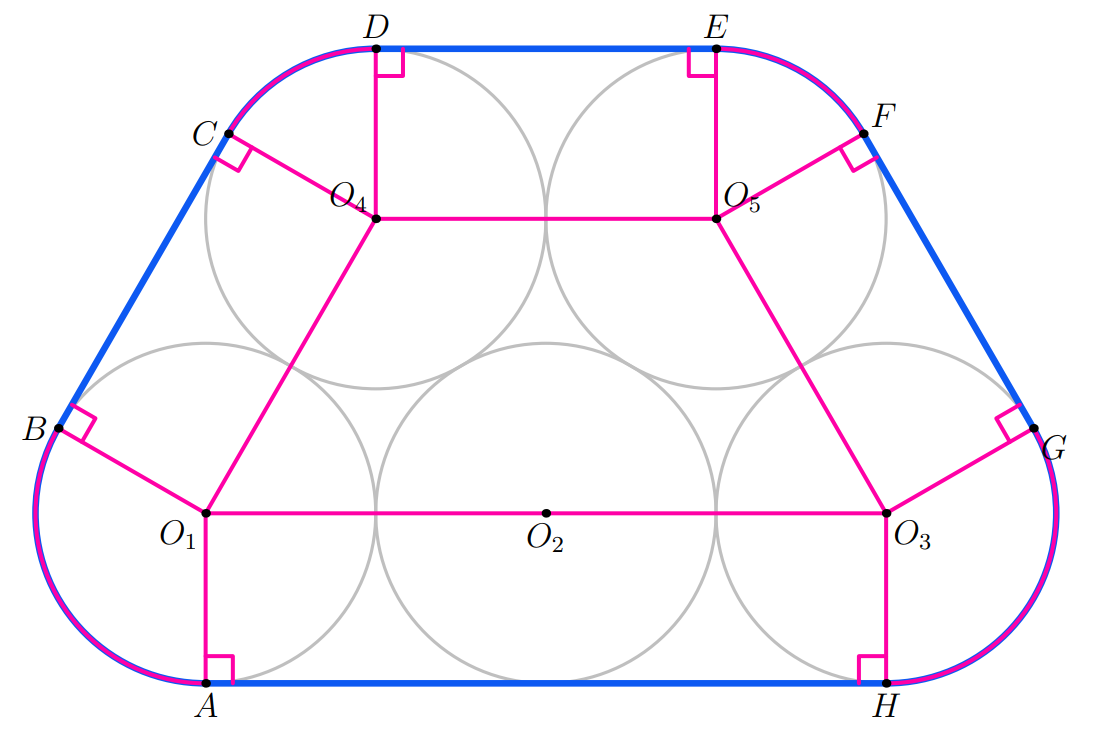
First, we can name the centers of the circles O1β,O2β,O3β,O4β,O5β as shown in the diagram above. Then we connect each center to the points of tangency on the outside of its circle, labeling those points A,B,C,D,E,F,G,H as in the diagram.
Since O4βD is a radius drawn to a point of tangency, it is perpendicular to the band at D. Hence β O4βDE is a right angle. Similarly, each radius drawn to a point of tangency is perpendicular to the band at that point, so
β AO1βO3β,β HO3βO1β,β HO3βO5β,β FO5βO3β,β HO5βO4β,β DO4βO5β,β CO4βO1β,β BO1βO4β
are all right angles.
Now, we've split the band up into 8 pieces: 4 straight sections and 4 curved sections. The straight segments are equal to the distances between the centers of the circles they connect, since a rectangle is formed between the two centers and two points of tangency (for example O4βO5βED is a rectangle). This means we can find all the lengths of the straight distances by adding up the radii. If the diameter of each circle is 4, then the radius is 2, which means:
DEBCFGAHβ=2β
2=4=2β
2=4=2β
2=4=4β
2=8β
So the sum of the lengths of the straight sections is 4+4+4+8=20.
For the curved sections, we can examine angles to find their lengths. Let the angle β CO4βD be xβ. Since the angles around center O4β must sum to 360β and we know both β DO4βO5β and β CO4βO1β are right angles, β O1βO4βO5β=360ββ90ββ90ββxβ=(180βx)β. O4βO5βO3βO1β is a trapezoid (since O4βO5β and O1βO3β are parallel) so β O4βO1βO3β+β O1βO4βO5β=180ββΉβ O4βO1βO3β=xβ. And symmetrically, β EO5βF=xβ,β O4βO5βO3β=(180βx)β, and β O5βO3βO1β=xβ. Thus, we also know that β BO1βA=β GO3βH=(180βx)β. Then looking at the sum of all of the inscribed angles of the arcs, we see that they sum up to 360β, since β BO1βA+β CO4βD+β EO5βF+β GO3βH=(180βx)β+xβ+xβ+(180βx)β=360β. Therefore, the total sum of the curved sections equals the length of the circumference of one circle or 4Ο, making our final answer equal to (C) 4Ο+20β.
The problems on this page are the property of the MAA's American Mathematics Competitions
