¶ 2026 AMC8 Problem 25
Problem:
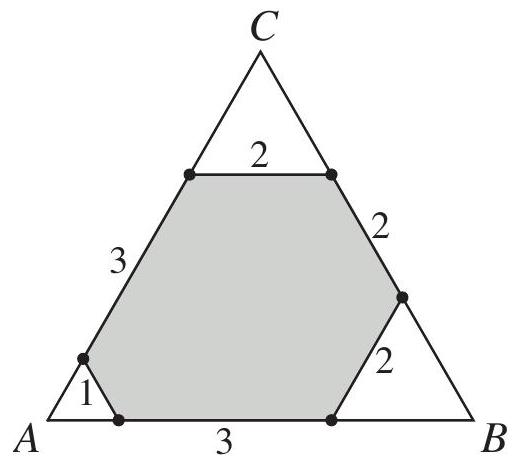
In an equiangular hexagon, all interior angles measure . An example of such a hexagon with side lengths of , and is shown below, inscribed in equilateral triangle . Consider all equiangular hexagons with positive integer side lengths that can be inscribed in , with all six vertices on the sides of the triangle. What is the total number of such hexagons? Hexagons that differ only by a rotation or a reflection are considered the same.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
First, we can find the side length of the outer equilateral triangle. Notice that each of the corners of the triangle outside of the hexagon are also equilateral triangles. So, from the example given, we see that the total side length is .
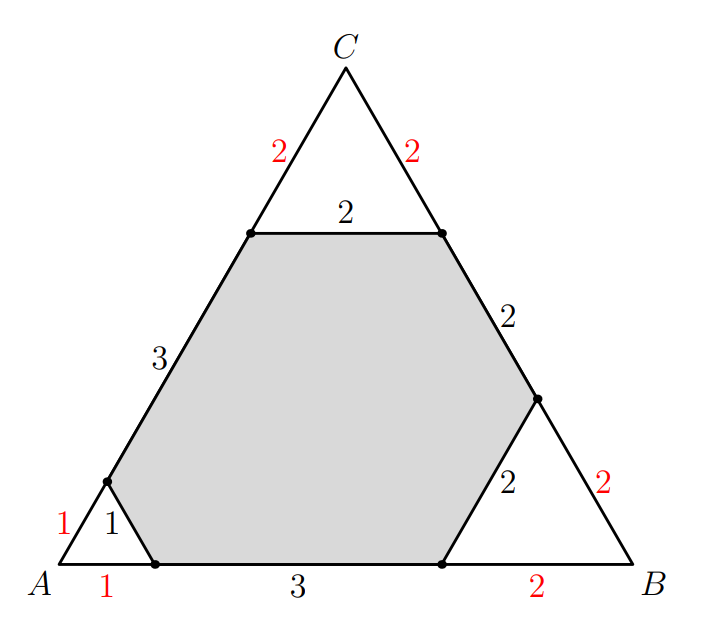
On each side of the equilateral triangle, the sum of the two corner segments and the hexagon side between them is . For the hexagon sides to be positive integers, the sum of any two adjacent corner cuts must be at most . Letting the corner cut lengths be , we require , , and . Each valid ordered triple determines a unique equiangular hexagon with side lengths . Two triples related by a rotation or reflection of produce congruent hexagons, so we classify these triples up to the dihedral symmetries of the triangle. Enumerating these equivalence classes yields exactly 8 distinct hexagons:
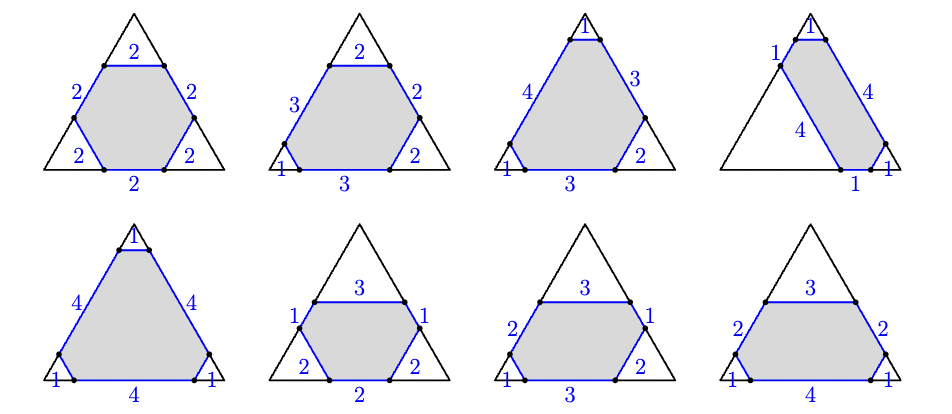
which gives us an answer of .
The problems on this page are the property of the MAA's American Mathematics Competitions