Problem: A point is selected at random inside an equilateral triangle. From this point perpendiculars are dropped to each side. The sum of these perpendiculars is:
Answer Choices:
A. least when the point is at the center of gravity of the .
B. greater than the altitude of the triangle.
C. equal to the altitude of the triangle.
D. one-half the sum of the sides of the triangle.
E. the sum is greatest when the point is the center of gravity.
Solution:
Let be an arbitrary point in the equilateral triangle with sides of length , and denote the perpendicular segments by .
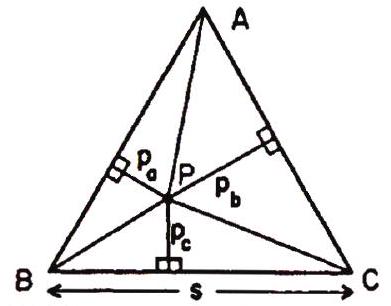
Then
Also, Area , where is the length of the altitude of . Therefore, and this sum does not depend on the location of .