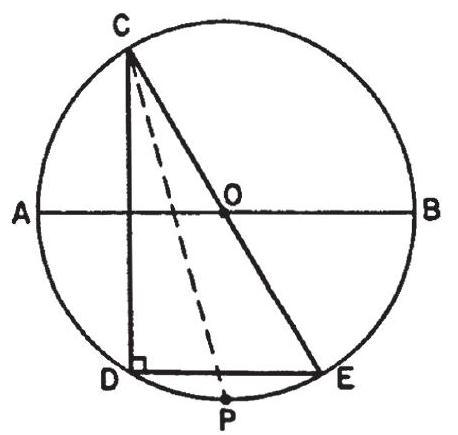
Problem: is a fixed diameter of a circle whose center is . From , any point on the circle, a chord is drawn perpendicular to . Then, as moves over a semicircle, the bisector of angle cuts the circle in a point that always:
Answer Choices:
A. bisects the arc
B. trisects the arc
C.
D. is as far from as from
E. is equidistant from and .
Solution:
Extend CO so that it meets the circle at . Since is a diameter, . The bisector of angle bisects the subtended arc , that is, arc . Regardless of the position of , the corresponding chord is always parallel to , and hence always bisects the arc .