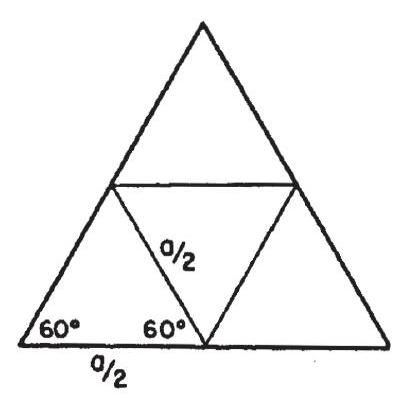
Problem: An equilateral triangle is drawn with a side of length a. A new equilateral triangle is formed by joining the mid-points of the sides of the first one. Then a third equilateral triangle is formed by joining the mid-points of the sides of the second; and so on forever. The limit of the sum of the perimeters of all the triangles thus drawn is:
Answer Choices:
A. Infinite
B. 541a
C. 2a
D. 6a
E. 421a
Solution:
Let Pk be the perimeter of the k th triangle.
Then Pk+1=21Pk.
S=P1+P2+P3+⋯=3a+21⋅3a+21⋅23a+⋯=3a(1+21+41+⋯)=3a1−(1/2)1=6a