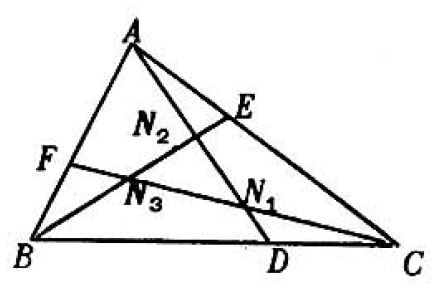
Problem: In the figure, CD,AE and BF are one-third of their respective sides. It follows that AN2:N2N1:N1D=3:3:1, and similarly for lines BE and CF. Then the area of triangle N1N2N3 is:
Answer Choices:
A. 101△ABC
B. 91△ABC
C. 71△ABC
D. 61△ABC
E. none of these
Solution:
By subtracting from △ABC the sum of △CBF,△BAE, and △ACD and restoring △CDN1+△BFN3+△AEN2, we have △N1N2N3.
△CBF=△BAE=△ACD=31△ABC.
From the assertion made in the statement of the problem, it follows that △CDN1=△BFN3=△AEN2=71⋅31△ABC=211△△ABC.
∴△N2N2N3=△ABC−3⋅31△ABC+3⋅211△ABC=71△ABC.