Problem: Two equal parallel chords are drawn inches apart in a circle of radius inches. The area of that part of the circle that lies between the chords is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
By symmetry, the required area is .
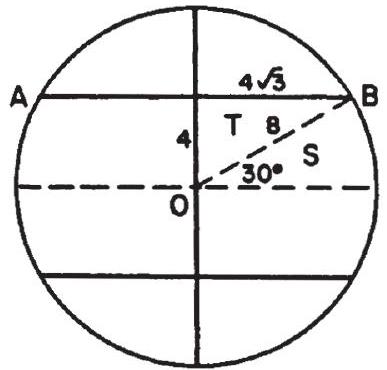
Problem: Two equal parallel chords are drawn inches apart in a circle of radius inches. The area of that part of the circle that lies between the chords is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
By symmetry, the required area is .
