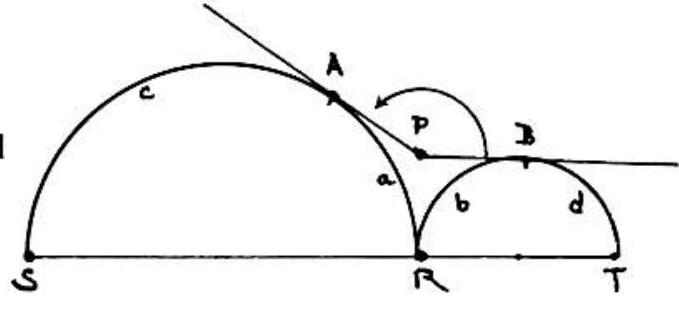
Problem: In the figure PA is tangent to semicircle SAR;PB is tangent to semicircle RBT;SRT is a straight line; the arcs are indicated in the figure. Angle APB is measured by:
Answer Choices:
A. 1/2(a−b)
B. 1/2(a+b)
C. (c−a)−(d−b)
D. a−b
E. a+b
Solution:
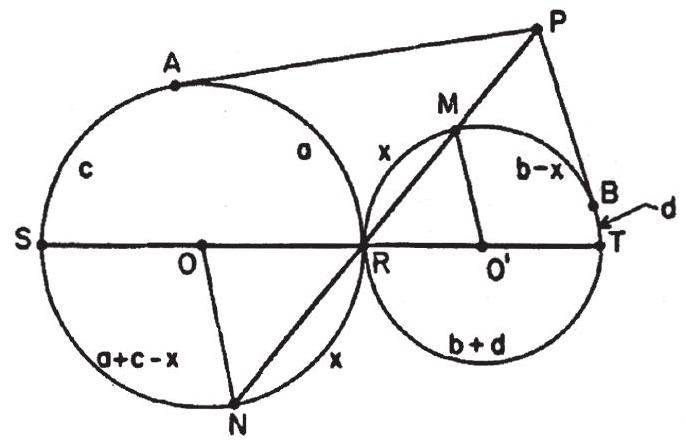
First, draw the line connecting P and R and denote its other intersections with the circles by M and N; see accompanying figure. The arcs MR and NR contain the same number of degrees; so we may denote each arc by x. To verify this, note that we have two isosceles triangles with a base angle of one equal to a base angle of the other. ∴∠NOR=∠MO′R.
∠APR=21{(c+a+c−x)−a}=21{2c−x}∠BPR=21{b+d+d−(b−x)}=21{2d+x}
and the sum of angles APR and BPR is
∠BPA=c+d.
The desired angle is
360∘−∠BPA=360∘−(c+d)=(180∘−c)+(180∘−d)=a+b.