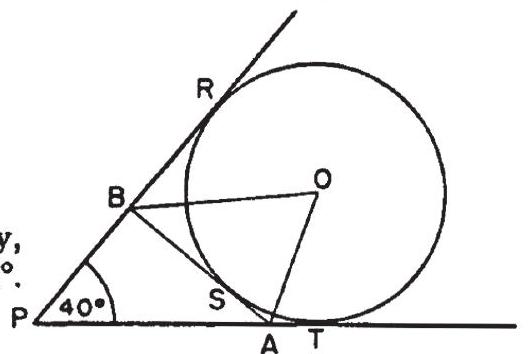
Problem: Triangle PAB is formed by three tangents to circle O. Angle APB=40∘, then angle AOB equals:
Answer Choices:
A. 45∘
B. 50∘
C. 55∘
D. 60∘
E. 70∘
Solution:
∠P=40∘;∴∠PAB+∠PBA=180∘−40∘=140∘.
∠TAS=180∘−∠PAB
∠RBS=180∘−∠PBA
∠TAS+∠RBS=360∘−140∘
=220∘.
Since OA and OB bisect angles TAS and RBS, respectively, ∠OAS+∠OBS=21(220∘)=110∘.
∴∠AOB=180∘−110∘=70∘
The number of degrees in ∠AOB is independent of the position of tangent ASB.
.jpg)
.jpg)
