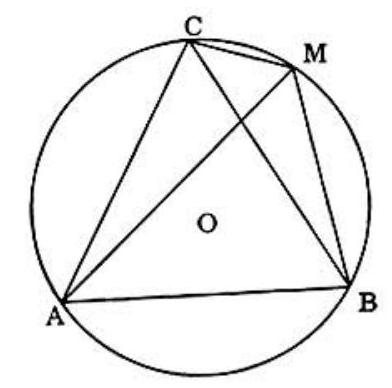
Problem: Let ABC be an equilateral triangle inscribed in circle O. M is a point on arc BC. Lines AM,BM, and CM are drawn. Then AM is:
Answer Choices:
A. equal to BM+CM
B. less than BM+CM
C. greater than BM+CM
D. equal, less than, or greater than BM+CM, depending upon the position of M
E. none of these
Solution:
Consider first the special case where M coincides with C. Then AM=AC and BM+MC=BM=BC=AC.
∴AM=BM+MC
To prove this in general, lay off MN (on MA) equal to MC. Since ∠CMA=60∘,△MCN is equilateral. We can show that △ACN≅△MCB because AC=CB,CN=CM, and ∠ACN=∠ACM−60∘=∠MCB.∴BM=AN and AM=AN+MN=BM+MC.